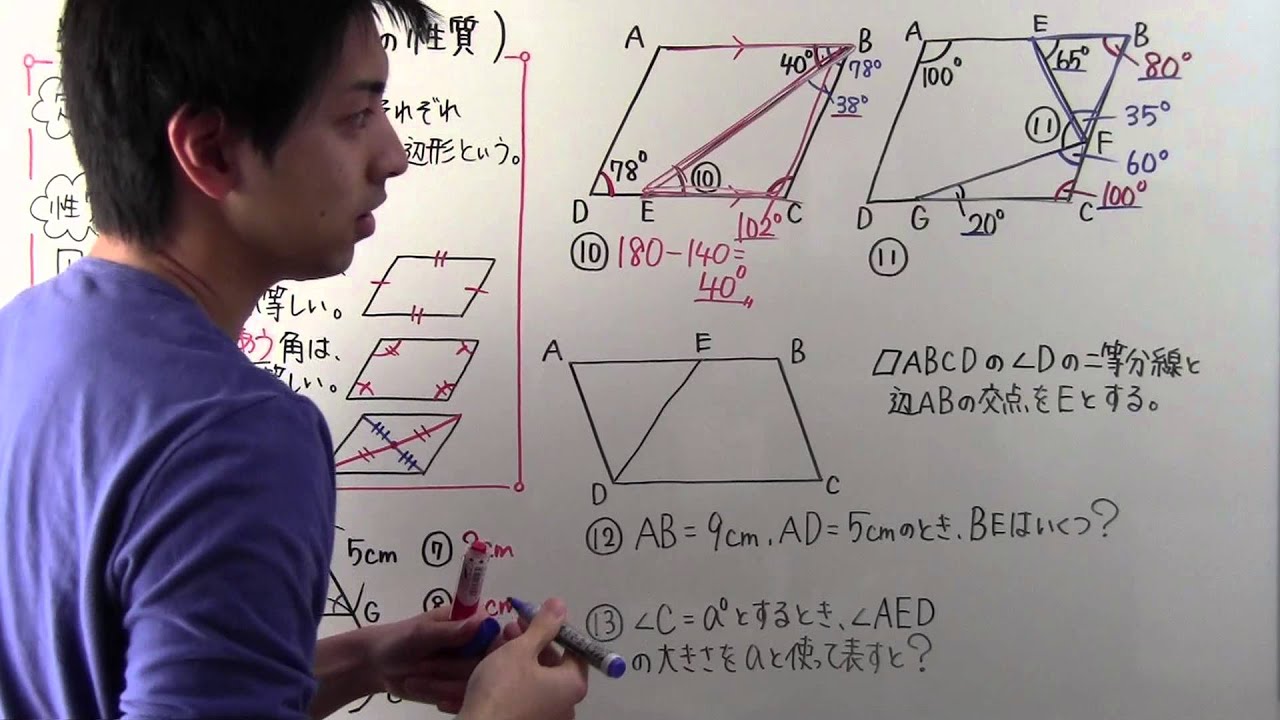
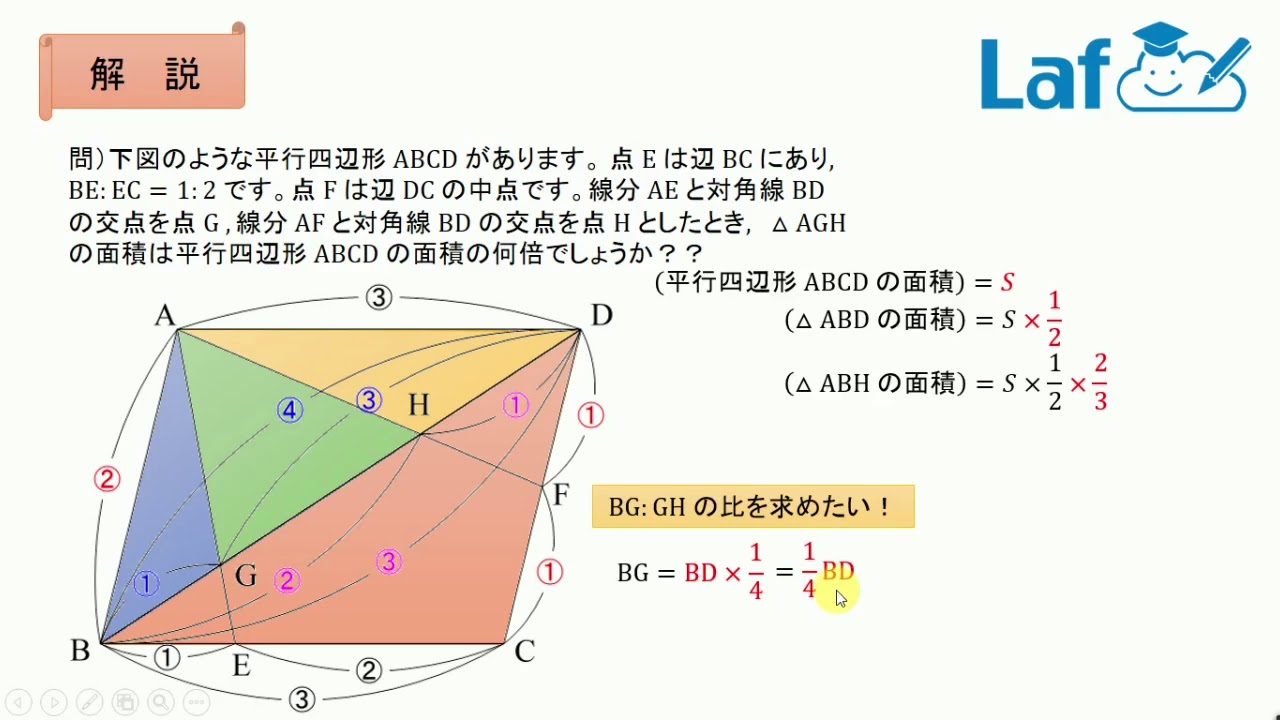
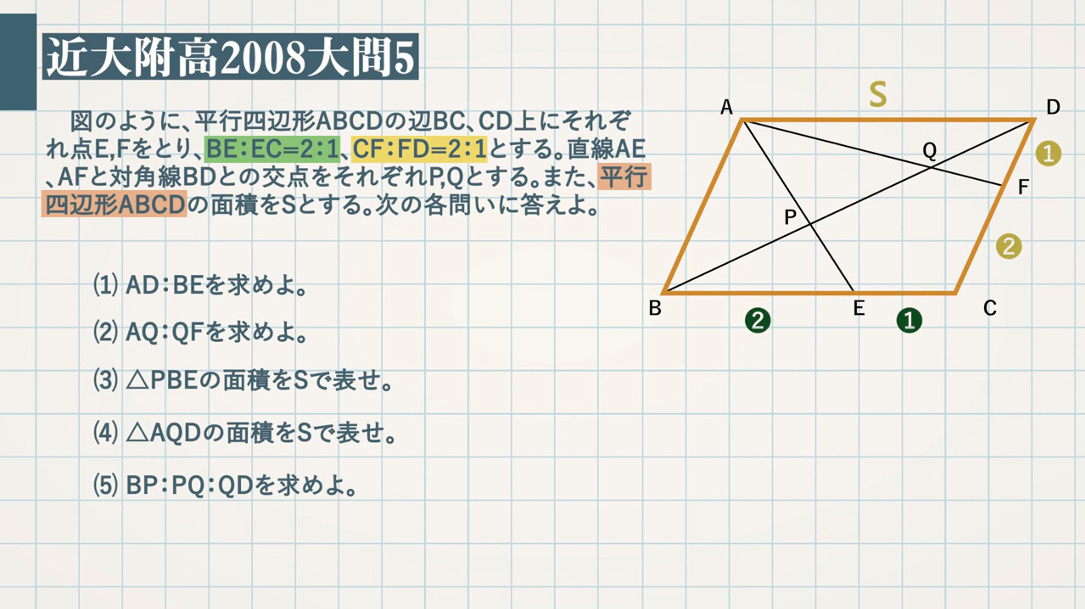
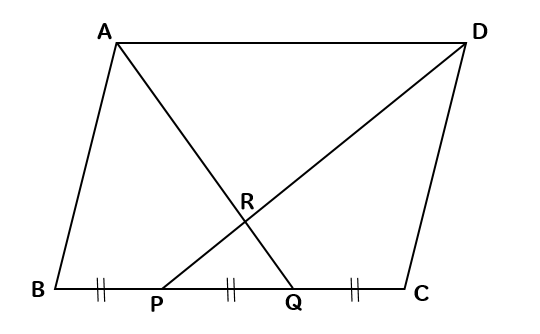
相似比の練習問題(平行四辺形1) 問1. (ア) (1) EFD ∽ CFB よりED:CB =EF:CF =1:3 CFD の面積=2 ×3 =6cm2 (2)BF:FD =3:1 より BCF の面積=6 ×3 =18cm2 or EFD ∽ CFB より相似比1:3 →面積比1:9 2 ×9 =18cm2 (3) ABCD の面積=(6 +18)×2 =48cm2 (イ) (1) FCD ∽ FEB 相似比は2:1 面積は4 倍 (2) FEB =5cm2 底辺の比=面積比=1:2 より FBC =5 ×2 =10cm2 相似比1:2 →面小学5年生の算数 三角形や平行四辺形の面積の問題プリントを無料ダウンロード・印刷 (プリント5枚) 小学5年生の算数 四角形の面積 台形・ひし形ほか 問題プリント 証明問題「平行四辺形であることの証明」 それでは、平行四辺形の条件を使って証明問題に挑戦してみましょう。 証明問題 四角形 の対角線の交点を とする。 このとき、 、 ならば、四角形 は平行四辺形となることを証明しなさい。 まずは、四角形 が平行四辺形であるためのどの条件に当てはまるかを考えましょう。 問題文中に という条件があるので、以下の つに絞れます。 組の向か
平行四辺形 算数解法の極意
平行四辺形 面積 問題
平行四辺形 面積 問題-全体の四角形も、台形のもの、長方形のもの、平行四辺形のものなどが考えられます。 今回は、全体が長方形のパターンで考えてみます。今回の問題パターンは、「 相似が見つけられる 」ということと、「 三角形の中の三角形の面積比 」を考えられるようになっていれば解けるはずです こんにちは。平行四辺形と面積②です。それではどうぞ。 面積比の問題で, 1つの攻略方法として, 相似比の2乗から攻める方法を紹介しておりますが, 相似な関係がない場合は, 役に立ちません。そこで, 相似な関係がなくてもで
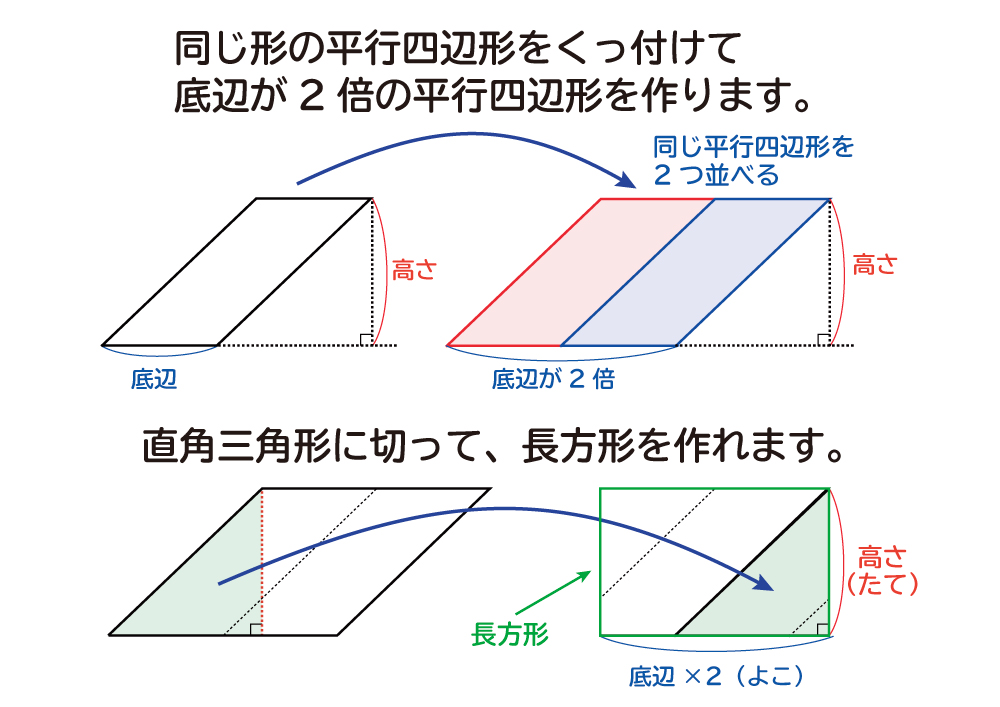



なぜ 平行四辺形の面積は 底辺 高さ なのか を説明します おかわりドリル
単元 三平方の定理 三角定規 15度 直角三角形 整数問題 証明問題 神奈川 平行四辺形 三平方の定理 円 直交する弦 相似 メネラウス 三平方の定理 神奈川 入試 平行線の錯角と同位角 循環小数・有理数・無限小数・41の倍数 中点連結定理 相似 内接円・外接円・三平方の定理 連立方程式 計算問題解説! 問題 下の図の平行四辺形ABCDで、BC上にBE:EC=3:2となる点Eをとり、AEとBDの交点をPとする。 PBEの面積が18㎠のとき、平行四辺形の面積を求めなさい。 平行四辺形の面積を求めたいのですが 全体を一度に求めようとすると難しいので 平行四辺形の半分に当たる ABDの面積を求めてやります。 その後、 ABDの面積を2倍してやれば平行四辺形が求められます以上で二つのベクトルが作る平行四辺形の面積は、それらのベクトル積の大きさに等しいことがわかりました。 ベクトル \(\overrightarrow{a} = \langle2, 0, 0 \rangle\) と \(\overrightarrow{b} = \langle 1, 1, 0 \rangle\) が作る平行四辺形の面積を求めよ。
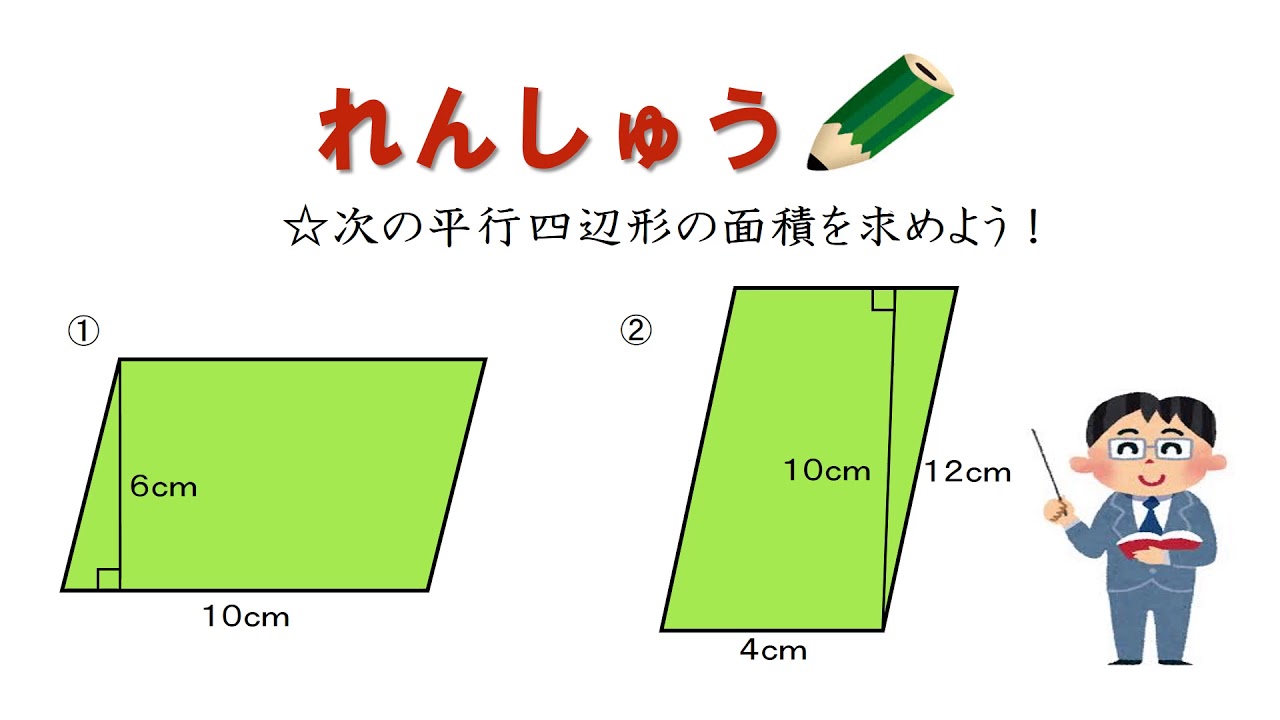
21年1月30日 このページは、 小学5年生が平行四辺形の面積について学習するための「平行四辺形の面積を求める問題集」が無料でダウンロードできる ページです。 この問題のポイント ・ 平行四辺形の面積は「底辺×高さ」で求めることができます。 ・平行四辺形の図形を見て、どこが「底辺」で、どこが「高さ」になっているか確認して面積を求めます。 ぴよ平行四辺形の面積を求める計算問題 底辺と高さから面積を求める問題 下の図に示した台形の面積を求めよ。 平行四辺形の面積を求める公式に代入して、計算するだけですね。 平行四辺形の面積 = 底辺 ×高さ = 6× 5 = 30cm2 平行四辺形の面積 = 底辺 × 高さ = 6 × 5 = 30 cm 2 となります。 底辺と高さを選んで面積を求める問題 下の図に示した台形の面積を求めよ。 この問題では、2種類の辺の管理人 11月 17, 18 小学校5年生で習う「平行四辺形」 の面積を求める問題集です。 問題をランダムで生成することができ、答えの表示・非表示も切り替えられます。 印刷してご活用ください。 ちなみに 平行四辺形 の面積の求め方についてはこちらに詳しく説明しています。 平行四辺形の面積の公式|なぜ『底辺×高さ』で求められるのか? 向かい合う辺が
21小数÷整数 22小数÷小数 3 面積 31平行四辺形の面積 32三角形の面積 33台形の面積 34ひし形の面積 35円の周の長さと面積 4 整数 平行四辺形の面積比の問題では, 平行四辺形の面積の半分 (1つの対角線で区切った三角形)を求めて2倍すれば, 平行四辺形の全体の面積が求めることができる。ケースバイケースであるかもしれないが, 半分を求めればいいという意識があるだけでも 見方は変わってくる。 その典型的な問題を2つ解いてみよう。 上の図で, 右の図で四角形ABCDは平行四辺形で, P東大寺学園中平行四辺形の問題 21年 5年生 6年生 入試解説 奈良 平行四辺形 東大寺 男子校 面積の差 ★★★★☆☆(中学入試難関校レベル)
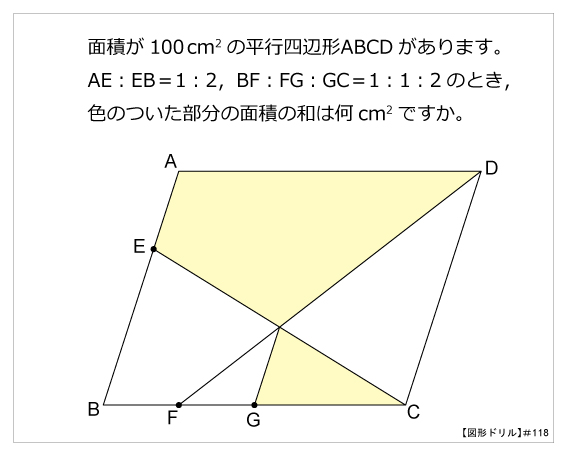



第118問 平行四辺形の面積の和 図形ドリル 第118問 平行四辺形の面積の和 算数星人のweb問題集 中学受験算数の問題に挑戦
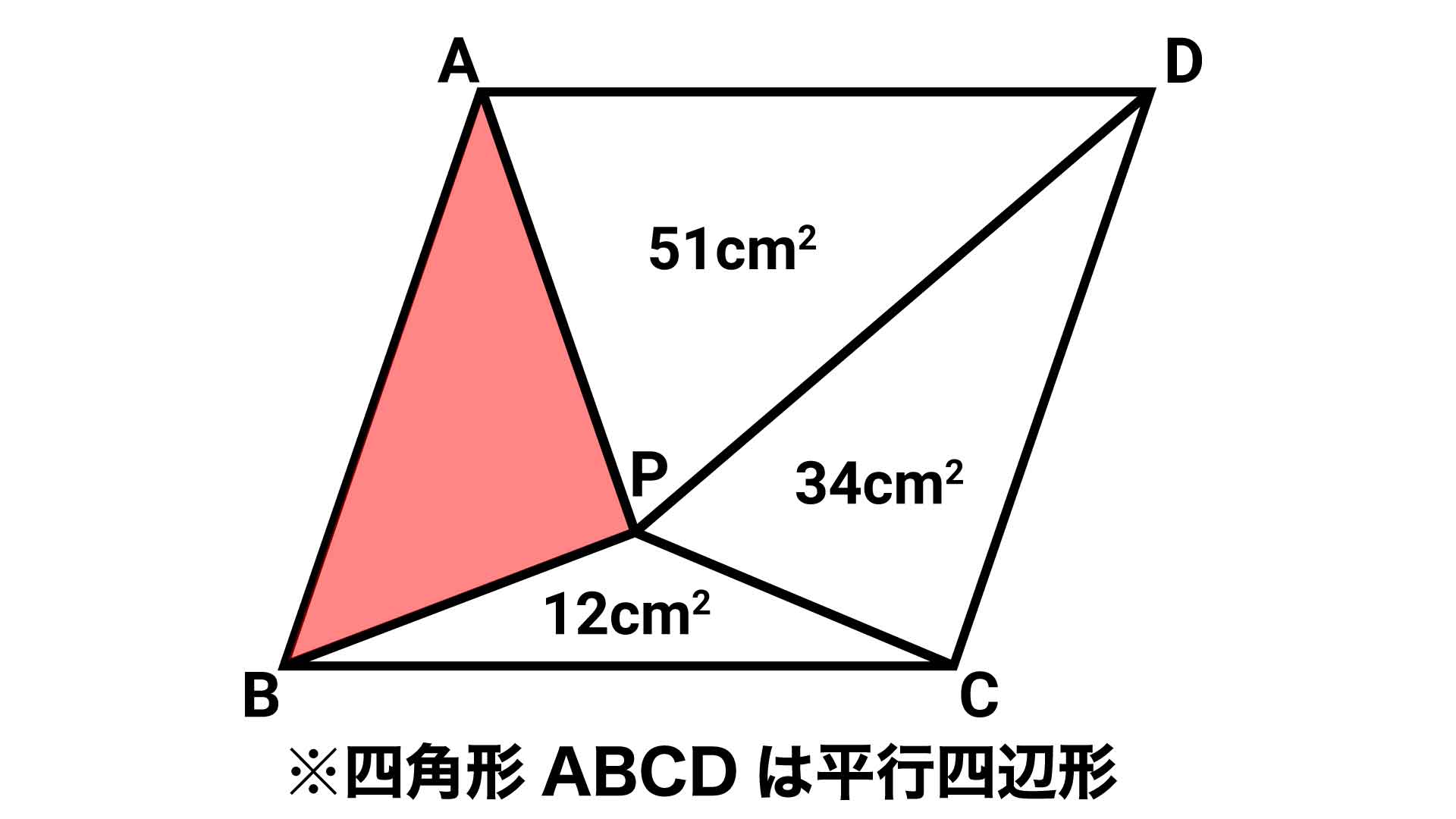



小学5年生で解ける 平行四辺形の面積 の問題 1分で解ける
平行四辺形の面積は,任意の直線で切断して長方形に等積変形すればよいことがわかり,求積す ることができる。 1問題場面をとらえる。 右の平行四辺形の面 積を求めましょう。 2面積の求め方を見通す。 「このままでは求められない。面積比 解説 図の平行四辺形abcdでeはabの中点、 bffc=53である。 このとき aegと四角形ebfgの面積比を求めよ。平行四辺形の面積もんだいは、底辺と高さを求めそれぞれを掛けるだけです すなわち 公式 底辺×高さ です 考え方は、面積のプリント①で説明しています 平行四辺形 面積問題 台形 面積 図形問題 小学5年生 台形の面積は、 公式 (上底+下底)×高さ÷2 です 上底と下底は、必ず平行です 高さは、平行な線に対して垂直に交わります 台形 面積問題 ひし形 面積 図形問 小学5年生 ひし形の面積は、 公式



攻略法 平行四辺形と面積 数樂管理人のブログ
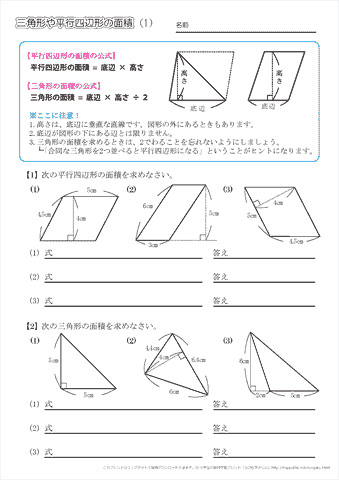



小学5年生の算数 三角形や平行四辺形の面積 問題プリント ちびむすドリル 小学生
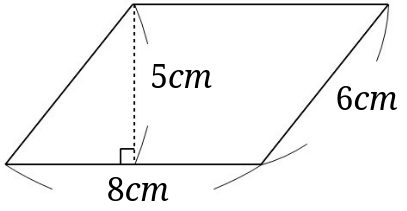
平行四辺形の面積を求めましょう。 平行四辺形の面積 名前 日にち 月 日 小学5年生 問題に答えましょう。 (1)高さが13cm,面積が117 ㎠である平行四辺形の底辺は何cm ですか。 ( ) (2)底辺が92m、面積が552 ㎡である平行四辺形の高さは何mですか。問題一括 (6,080Kb) 解答一括 (6,744Kb) 平行線と角 (2) 平行線と角 (3) 三角形の内角と外角 (1) 三角形の内角と外角 (2) 三角形の内角と外角 (3) 平行四辺形の面積=底辺×高さ となります。 これは、長方形を移動した平行四辺形の面積(たて×横)と同じになることから考えることができます。 次のような問題がよく出題されます。 底辺と高さがどこか注意して間違えないようにしましょう。 下の平行四辺形の面積を求める。 底辺は3cm 高さは5cmになります。 他の長さと間違えないようにし




算数パズル 10秒で解けますか 公式を使わない平行四辺形の面積問題 Youtube
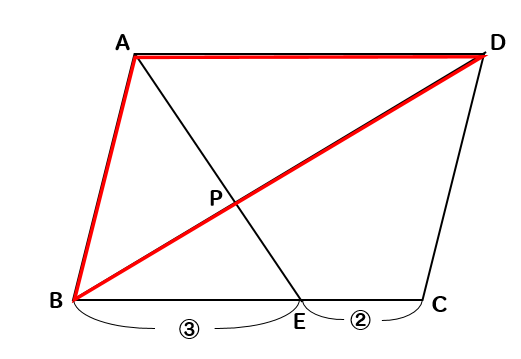



相似 平行四辺形と面積比の問題を徹底解説 数スタ
三平方の定理 例題 三平方の定理 三平方の定理2 三平方_平行四辺形の対角線 特別な直角三角形_補助線が必要な問題 二等辺三角形の面積 台形の面積 三平方_三辺の長さから三角形の面積を求める 三平方_2点間の距離 三平方_座標平面の三角形 三平方_座標(最短距離) 三平方_座標(点と直線の距離この平行四辺形の面積を、「底辺×高さ」から求めようとするのは 無謀ですね。 下のように、よく知った三角形 2 2 つに分けるのが楽なパターンです。 AB A B を通る直線の式が y = −x6 y = − x 6 と簡単に求まるので、 この直線の y y 切片は 6 6 です 平行四辺形の面積 平行四辺形の面積の問題です。 公式は難しいものではありませんが、底辺と高さをしっかり理解するようにしてください。 ポイント 平行四辺形の1つの辺を底辺とするとき、底辺に向かい合う辺まで垂直にひいた直線の長さを高さといいま 15年11月16日 / Last updated 19
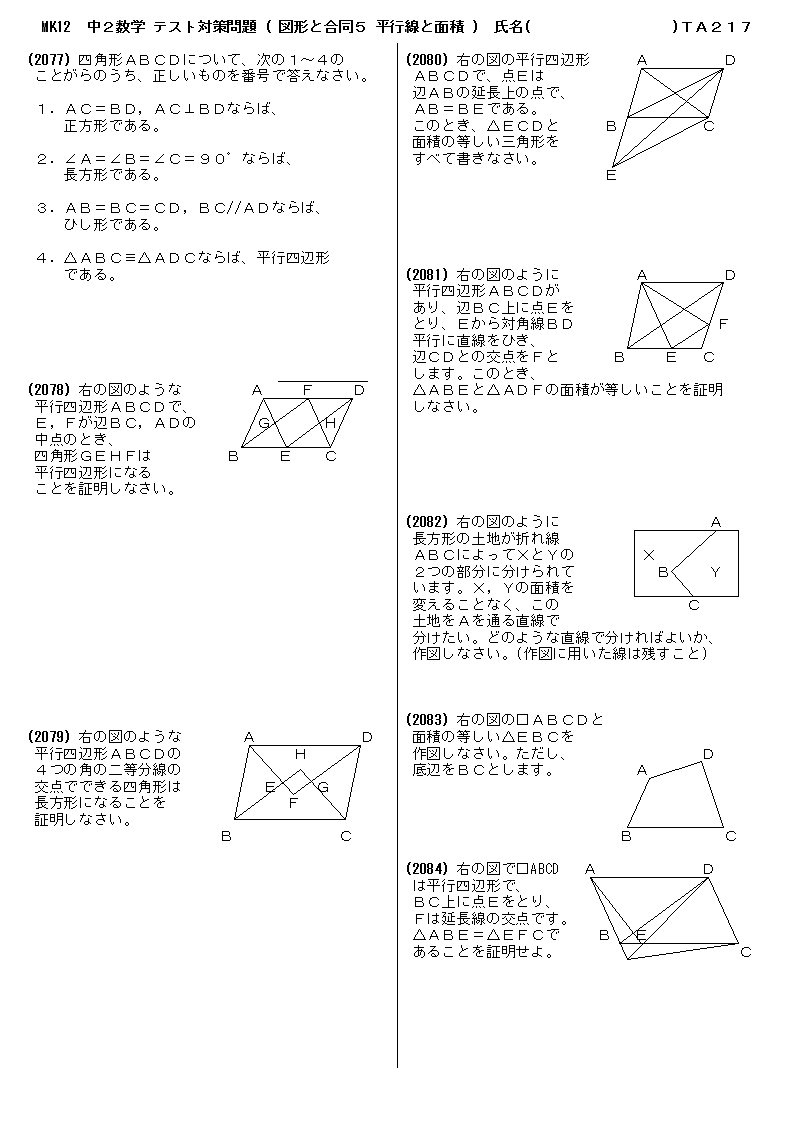



無料 中2数学 テスト対策 問題プリント 217 図形と合同5 平行線と面積
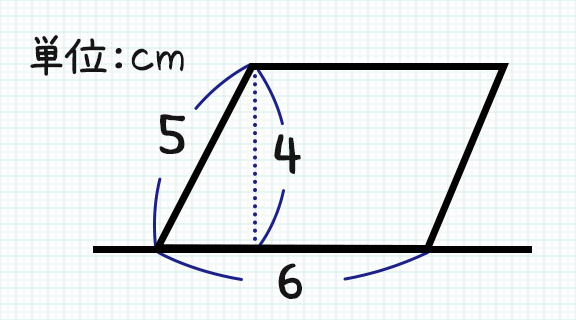



毎日脳トレ この平行四辺形の面積わかる Dアプリ レビュー
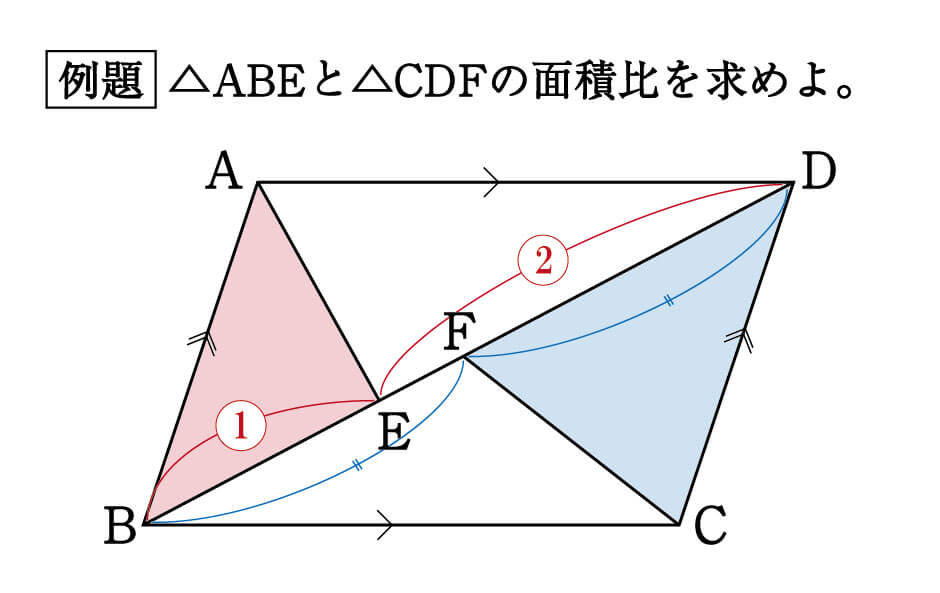
平行四辺形と長方形の面積は同じになるので、平行四辺形の道の面積も右端に寄せてしまいます。 中の長方形の面積を求めます。 ×30=600㎡ 例3)頂点をまとめて考えます。 *平行四辺形の中の色のついた部分の面積を求めます。 頂点をまとめると下の図 上図のように正三角形10個で作られた平行四辺形があります。 この平行四辺形の面積は300㎠です。 ここで問題です。 青色部分の面積を求めてください。 見た目は面白そうですが使う知識は数学の相似やら面積比やら、ごりごりに数学です。問題の解説&答え それでは、上で説明した特徴を活かして 平行な線に注目しながら 面積の等しい三角形を見つけていきましょう! まず、四角形ABCDは平行四辺形なので それぞれの向かい合う辺が平行になるということがわかります。 そして、このAD//BCを利用して FDを底辺とする三角形に注目すると CDF= BDF



平行四辺形の面積 算数 一般常識クイズ一問一答問題まとめ
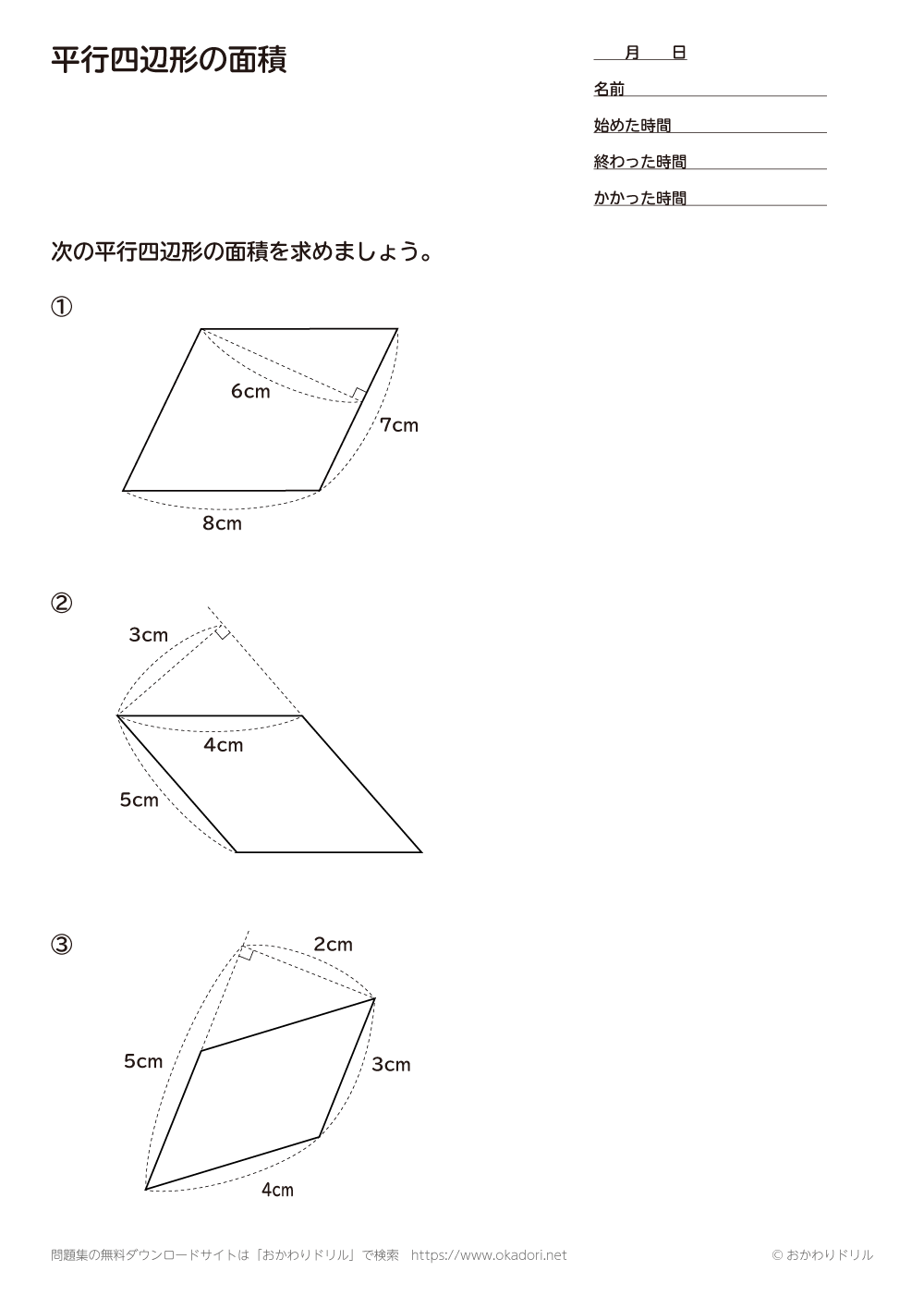



小学5年生 算数 無料問題集 平行四辺形の面積 おかわりドリル
平行四辺形の中の三角形の面積の問題ですが・・・。 平行四辺形abcdについて 辺ad,bcを21に内分する点をe,fとすると 三角形s1~s4の面積の合計は 平行四辺形の面積の①倍である。 答え 7/18倍 よろしくお願いします。第292問 平行四辺形の面積 図形ドリル 5年生 6年生 平行四辺形 相似 相似比 面積比 ★★★★☆☆(中学入試難関校レベル) 思わず「お~~!!」と言いそうな良問を。受験算数の定番からマニアックな問題まで。図形ドリルでは,色々なタイプの図形 小学5年生算数で習う 「四角形と三角形の面積」「面積の求め方を考えよう」「図形の面積」の無料学習プリント (練習問題・ワークシートドリル・テスト) です。 平行四辺形、三角形、台形、ひし形など基本の面積を求める問題から複雑な難しい応用編の面積問題も用意しました。 今回は、面積問題によく登場する四角形と三角形の面積の公式もご紹介し



数学 中2 73 平行四辺形の性質 Youtube



攻略法 平行四辺形と面積 数樂管理人のブログ
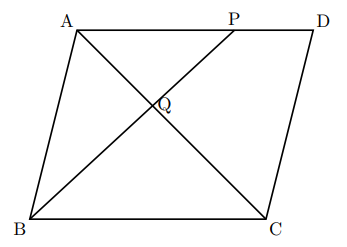
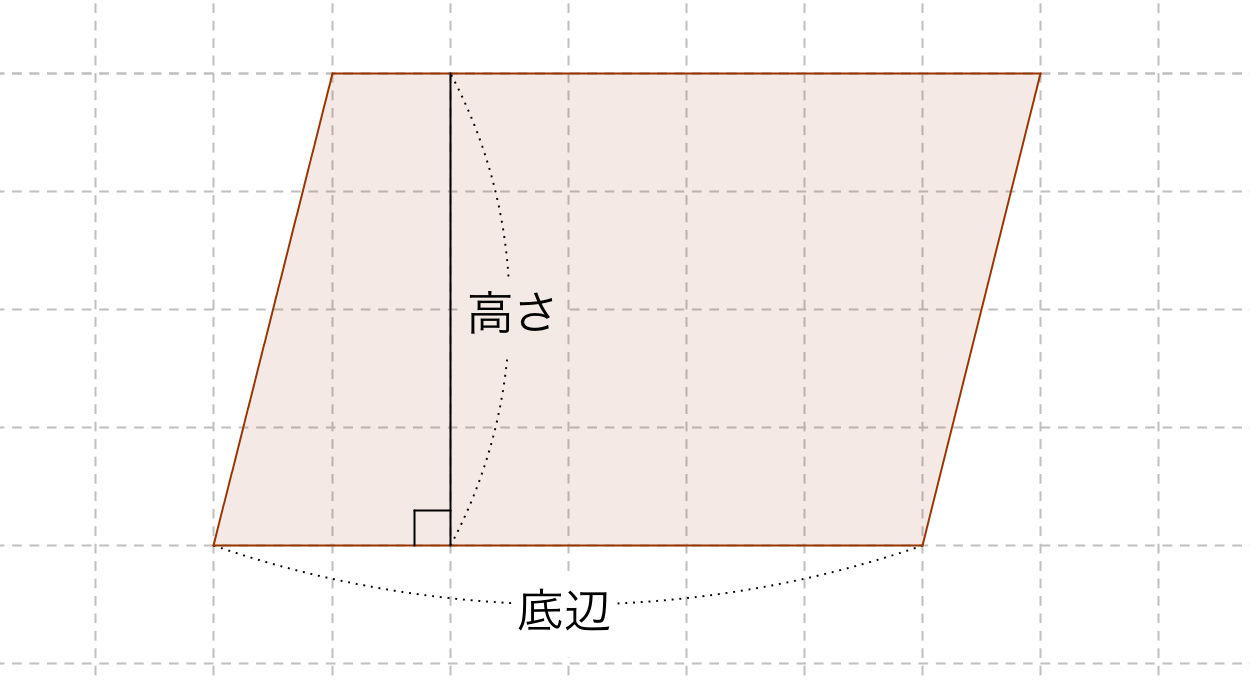
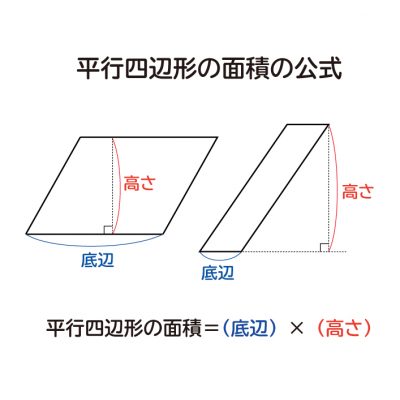
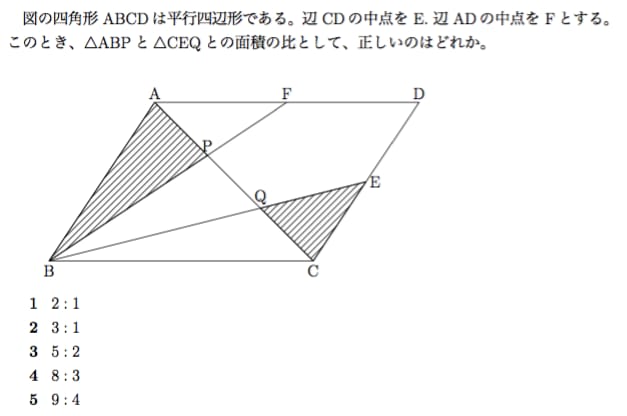
平行四辺形 は、三角形をひっくり返して足したのと同じです よって、三角形の面積は 底辺×高さ÷2 平行四辺形の面積は 三角形の面積×2なので (底辺×高さ÷2)×2 = 底辺×高さになります 平行四辺形面積の公式を忘れても、考え方を覚えていれば大丈夫です ↓面積・体積 問題のTOPページはこちら 面積比の基本練習問題 図のように、ab=4cm、bc=6cmの平行四辺形abcdがあり、点eは辺cdを1:3に分ける点である。また、点pは線分acとbeの交点である。このとき、 abpと平行四辺形abcdの面積の比を求めよ。 面積比の基本練習問題(解説・解答) 解説 最初の図の公式 を利用 よって平行四辺形の面積は、 7× 3√11 2 7 × 3 11 2 = 21√11 2 = 21 11 2 不明点があればコメント欄よりお願いします。 スポンサーリンク 図形と証明 中学3年生, 難易度★★ Posted by



中3数学 相似な図形 三角形の面積は平行四辺形の面積の何倍 Youtube



平行四辺形と比 教遊者
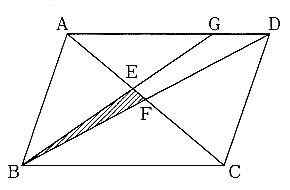
最後に平行四辺形の面積は対角線で区切った三角形 abdの2倍になります。 よって、30×2=60で60㎠と答えが求まります。 まとめ この問題に慣れて頭の中ですらすら解いていけるようになるとめっちゃ面白いです。 すぐ飽きますけど。笑平行な線と辺bcとの交点をfとする。 e cdfと同じ面積の三角形を すべて答えなさい。 b c 面積が ㎠の平行四辺形で、点 を次のようにとるとき、 以下の問いに答えなさい。 ① a p d② a d b c b p bpcの面積 bp のとき pdcの面積 解答 acdと bcd abcと abd 1 /4点 2 1 e 3 60 p c底辺と高さが等しいと、面積も等しくなります。 1:10 例題 1 右の平行四辺形 A B C D で、 A C / / E F のとき、 A C E と面積の等しい三角形をすべて答えなさい。 STEP 1 :各辺を底辺として、等しい三角形を探す ① A C を底辺と考えた場合 A C / / E F より、 A C F ② A E を底辺と考えた場合 A E / / D C より、 A D E ③ C E を底辺と考えた場合 平行な線がないので、面積の



平行四辺形を分ける面積比の求め方 算数解法の極意



北辰塾 情報局 直撃 中学入試問題 第53回 鴎友学園女子中 面積比の問題
平行線と面積に関する問題は以下のことをしっかり確認しておきましょう。 平行線にはさまれた三角形の面積は等しい 面積が等しい三角形の頂点を通る直線は平行 例)下の図で ABCと DBC面積が等しい → ABC= DBC とかく。 等積変形の問題 平行線と面積を利用して補助線を引いて面積が等しいことを証明したり、面積が等しい図形を作図する問題が出題され 平行四辺形の面積を二等分する直線を求める練習問題です。 ここで差がつく! 平行四辺形の性質を理解しているか。 特に、関数の問題においては、 平行四辺形は向かい合う線分は平行なので、「傾き」が同じ である。 平行四辺形の面積を2等分する直線は、必ず「対角線の交点」を通る。 目次 平行四辺形の面積を二等分する直線を求める練習問題 平行四辺形の面積を二等分する直線をスポンサーリンク 平行四辺形の面積 \(=\) 底辺 \(\times\) 高さ それでは「平行四辺形の面積の公式」を使った「練習問題」を解いてみましょう。「公式の考察」についても合わせてみていきます。 練習問



平行四辺形の面積の公式 算数の公式
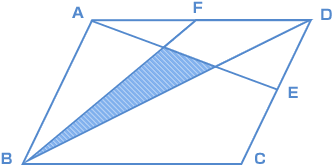



算数 平面図形と比 1 中学受験 ベネッセ教育情報サイト




平行四辺形の面積の求め方 公式と計算例



3




平行四辺形の面積を求める公式 あまり知られていないかも 中学や高校の数学の計算問題




5年生算数ドリル 面積
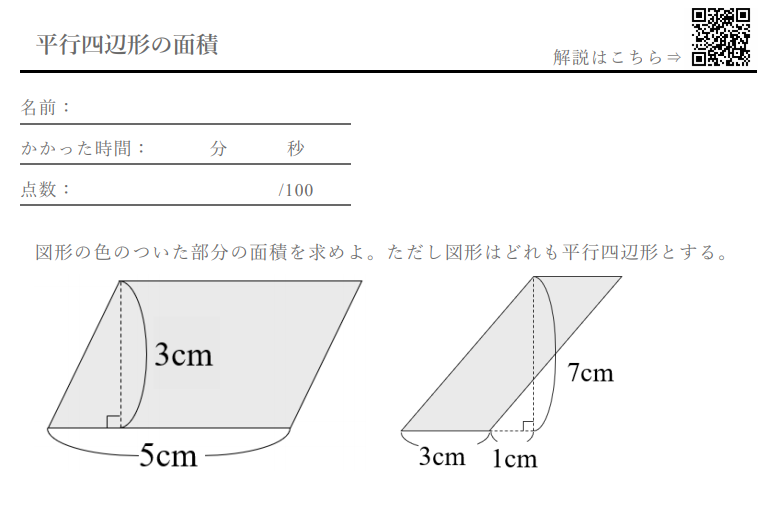



平行四辺形 の面積 計算ドリル 問題集 数学fun




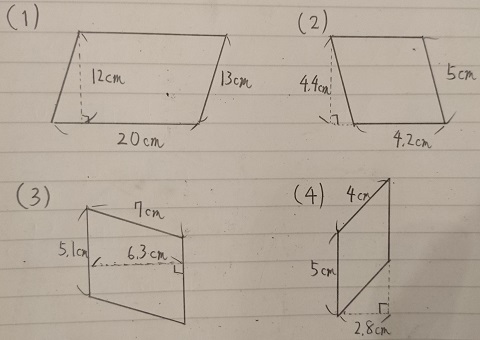
小学5年生の算数 四角形の面積 台形 ひし形ほか 問題プリント ちびむすドリル 小学生



3
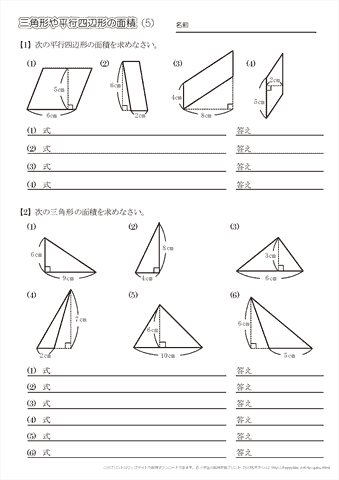



小学5年生の算数 三角形や平行四辺形の面積 問題プリント ちびむすドリル 小学生
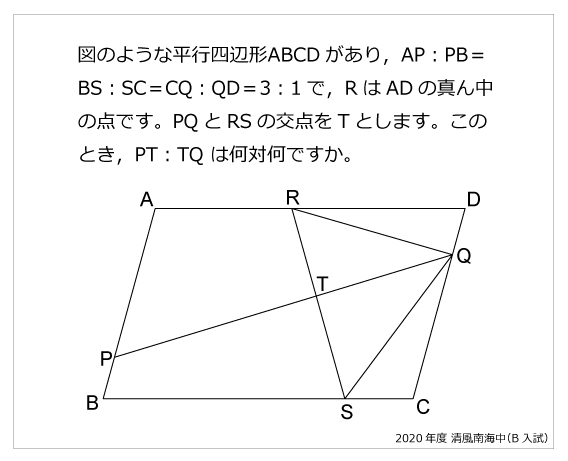



平行四辺形 算数星人のweb問題集 中学受験算数の問題に挑戦




平行四辺形のなかの三角形の相似や角度 長さ 等しい面積の求め方 現役塾講師のわかりやすい中学数学の解き方



相似 平行四辺形と面積比の問題を徹底解説 数スタ



小学生 算数 公式の解説一覧 おかわりドリル
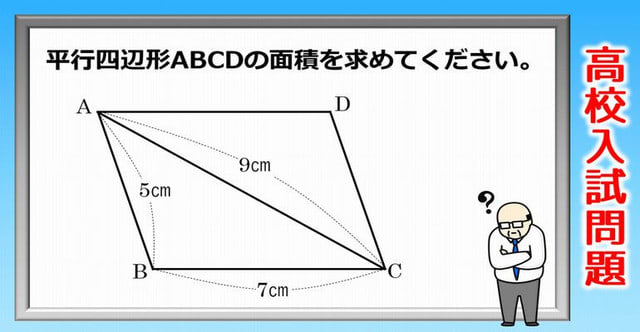



高校入試 シンプルですが悩んでしまう平行四辺形の面積の良問 暇つぶしに動画で脳トレ



小5 面積の求め方を考えよう 平行四辺形の面積の求め方 日本語版 Youtube




なぜ 平行四辺形の面積は 底辺 高さ なのか を説明します おかわりドリル




パパしゅく 算数 5年生 平行四辺形の面積 平行四辺形の色のついた面積を求める問題を作成しました 詳しくはパパしゅくをご覧ください Sites Google Com Site Shogakutezukurimondaishu Home 5nensei Muke Tedzukuri Mondai Shuu
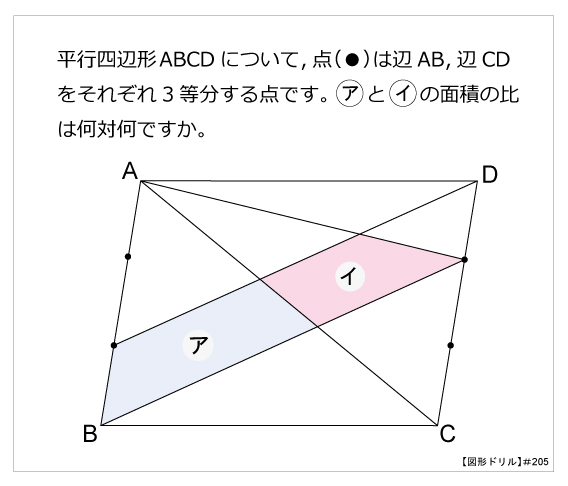



第5問 平行四辺形内の面積比 図形ドリル 第5問 平行四辺形内の面積比 算数星人のweb問題集 中学受験算数の問題に挑戦




小学5年生 算数 無料問題集 平行四辺形の面積 おかわりドリル




ひし形の面積の公式 小学生に教えるための分かりやすい解説 数学fun
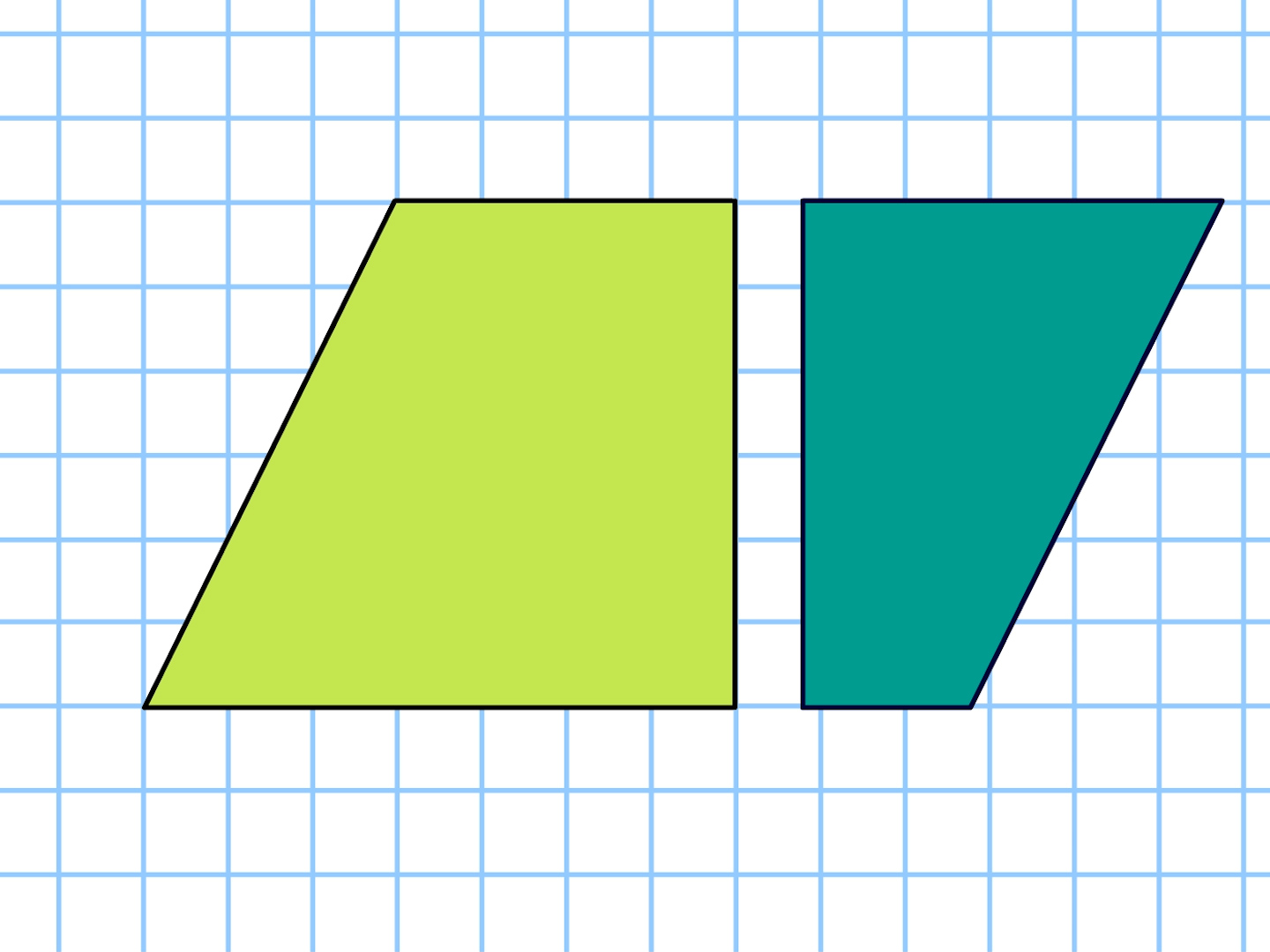



5年 平行四辺形の面積 算数イメージ動画集 大日本図書




平行四辺形の面積の求め方 公式と計算例



今月の問題 平行四辺形の中の三角形の問題



1




等積変形を用いる面積問題 14年 早稲田中学校 恋する中高一貫校 適性検査 徹底攻略



平行四辺形 算数解法の極意




平行四辺形の面積の求め方 公式と計算例



Tikz 年度 群馬県前期の問題 平行四辺形と面積 数樂管理人のブログ



平行四辺形の面積比 イメージでわかる中学受験算数問題



正方形の中の平行四辺形 桐蔭学園中学 09年 これが中学入試に出た図形問題
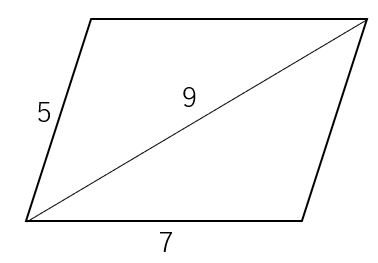



面積 平行四辺形の面積の変わった求め方の問題 数学の要点まとめ 練習問題一覧




高校数学 平行四辺形の面積の求め方 例題編 映像授業のtry It トライイット




等積変形を用いる面積問題 14年 早稲田中学校 恋する中高一貫校 適性検査 徹底攻略



図形問題が驚くほど得意になる基本問題とは あおぞら塾
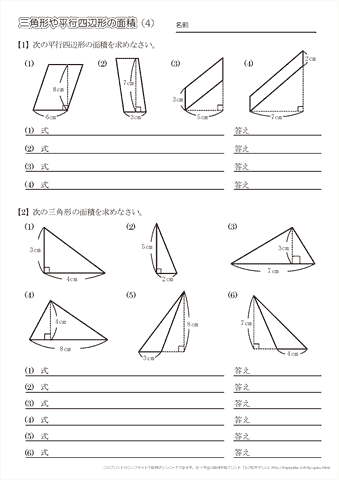



小学5年生の算数 三角形や平行四辺形の面積 問題プリント ちびむすドリル 小学生



攻略法 平行四辺形と面積 数樂管理人のブログ




面白い数学の問題 きれいな平行四辺形 ビジュアルで選んだらとんでもない目に合った そらの暇つぶしch



数学 なぜ面積比は苦手になりがちなの 面積比 集中特訓 1 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




高校入試対策数学 平面図形問題 相似の証明 平行四辺形と面積比の問題 Youtube




5年生算数ドリル 面積
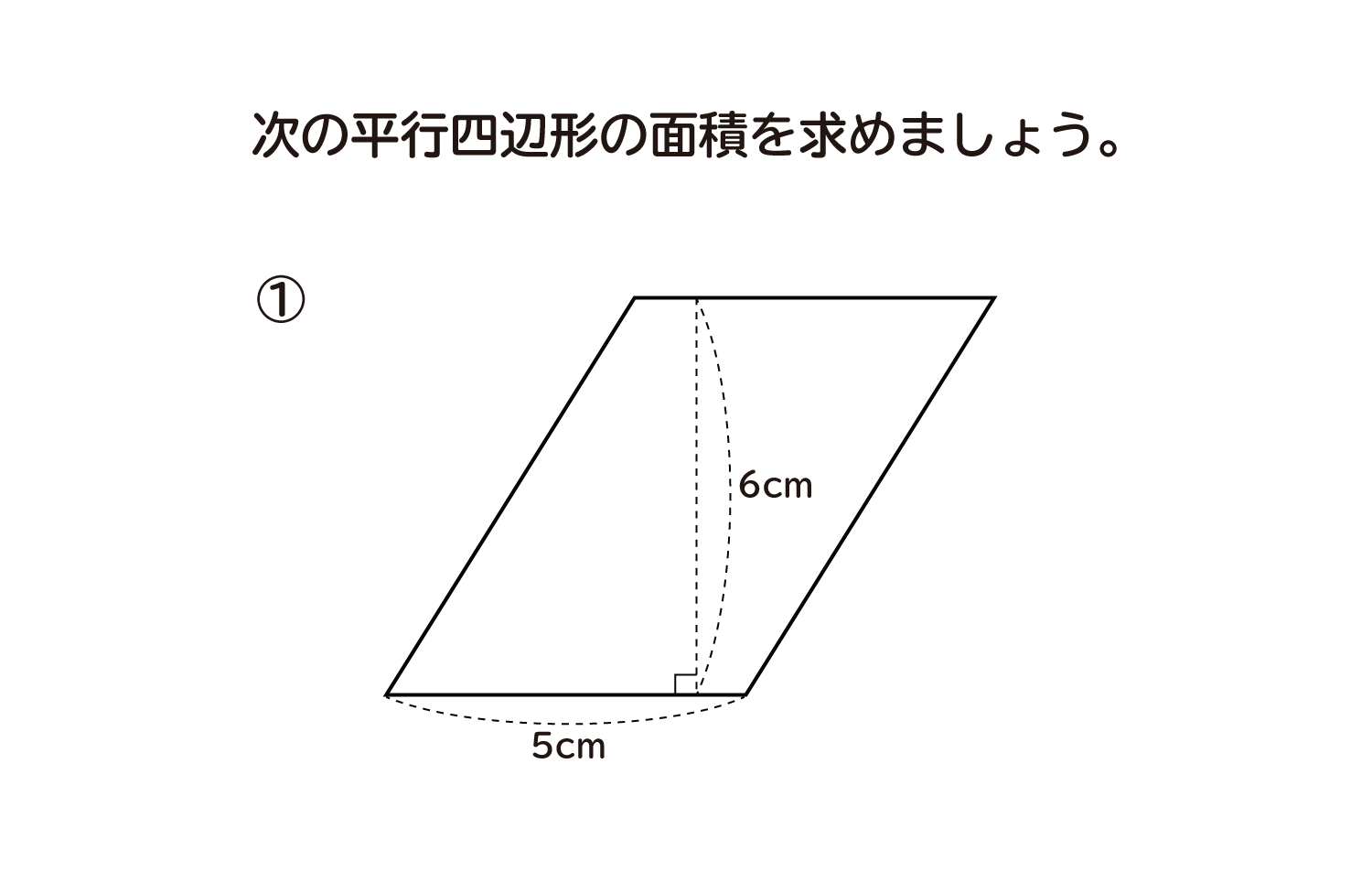



小学5年生 算数 無料問題集 平行四辺形の面積 おかわりドリル




面積問題 小学4から6年生 算数問題プリント




相似 平行四辺形と面積比の問題を徹底解説 数スタ



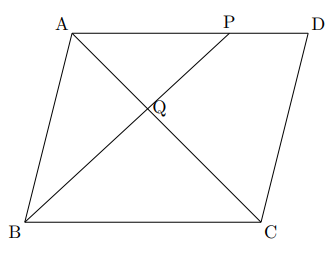
平行四辺形 中点 2つの三角形の面積比 知能問題 数的処理 判断推理 数的推理 数学パズル spi 空間把握 解いてみてください
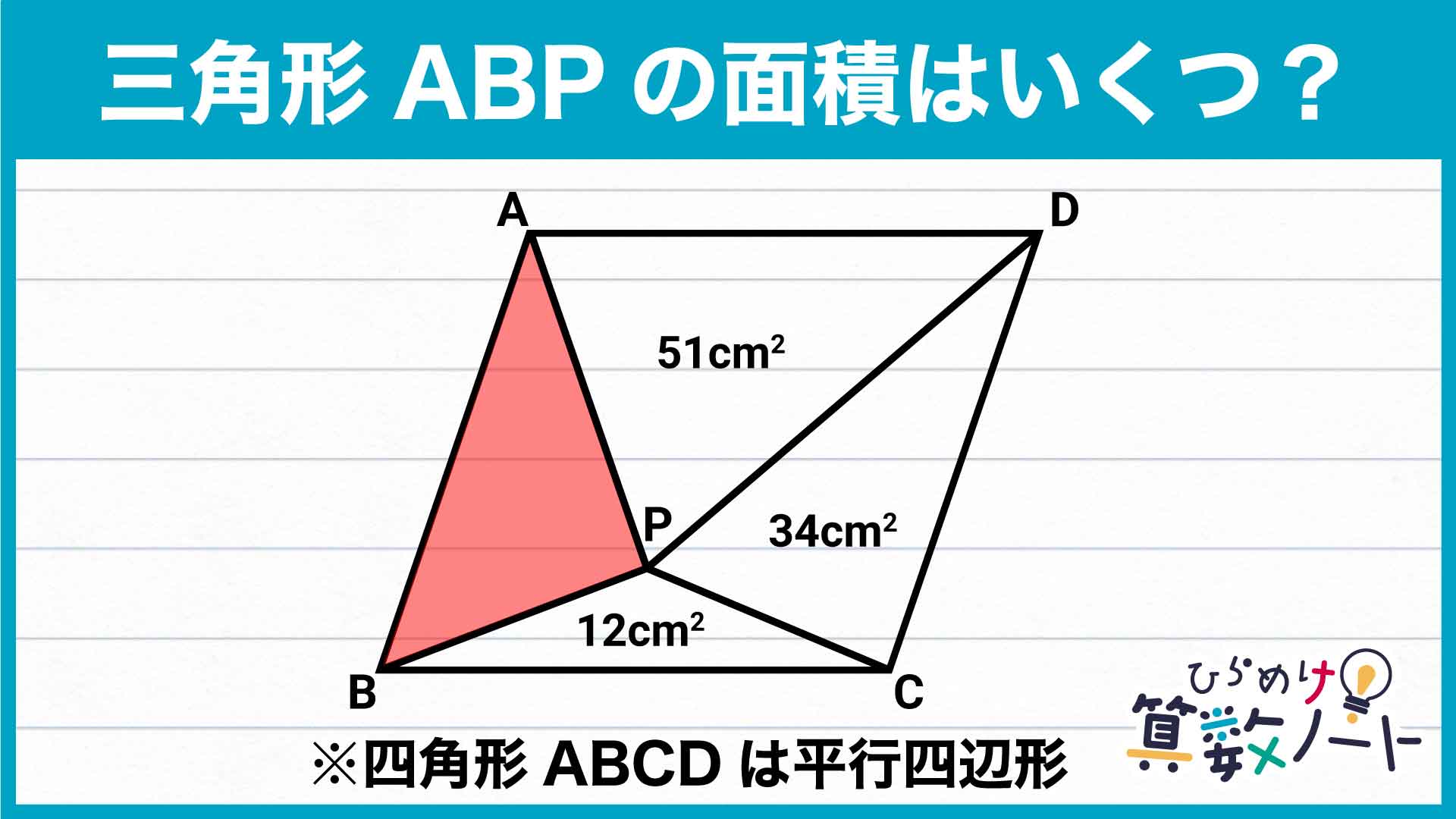



小学5年生で解ける 平行四辺形の面積 の問題 1分で解ける




面積 平行四辺形の面積 01 高さが外にあるときの面積の求め方 Youtube




中学受験算数 平行四辺形の面積を求める問題 Okwave



平行四辺形の部分面積は パズル算数クイズ




高校数学 平行四辺形の面積の求め方 練習編 映像授業のtry It トライイット




平行四辺形の面積の求め方 公式と計算例




平行四辺形の面積を求めるある問題について 身勝手な主張



1



平面図形と比 平行四辺形の面積比 Next Stageのブログ
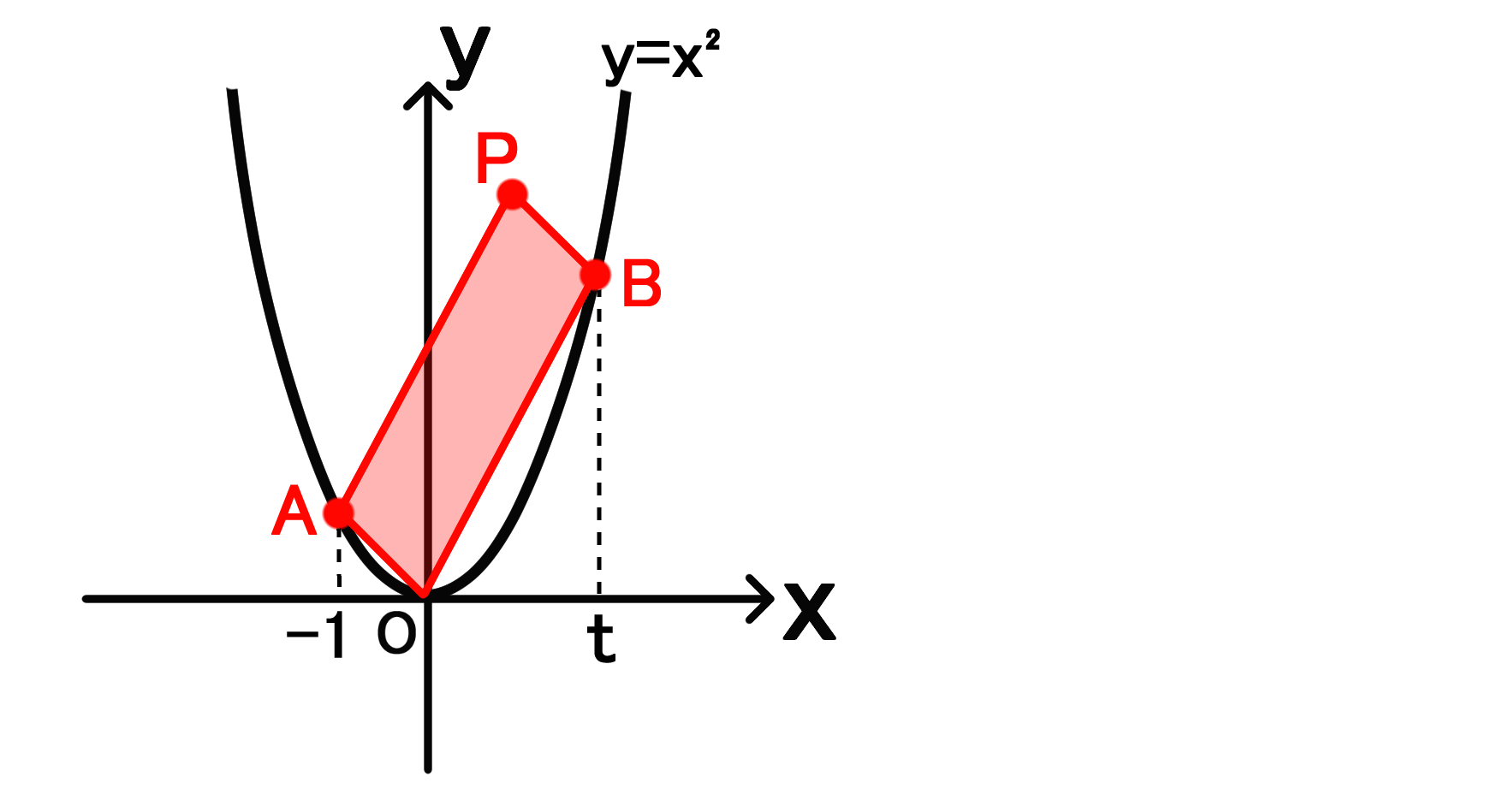



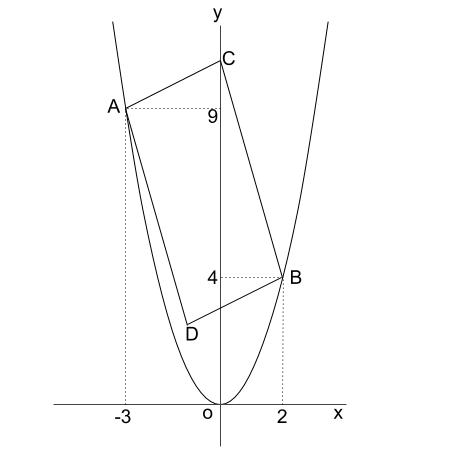
放物線y X 上の点を結ぶと平行四辺形になる問題 バカでもわかる 中学数学
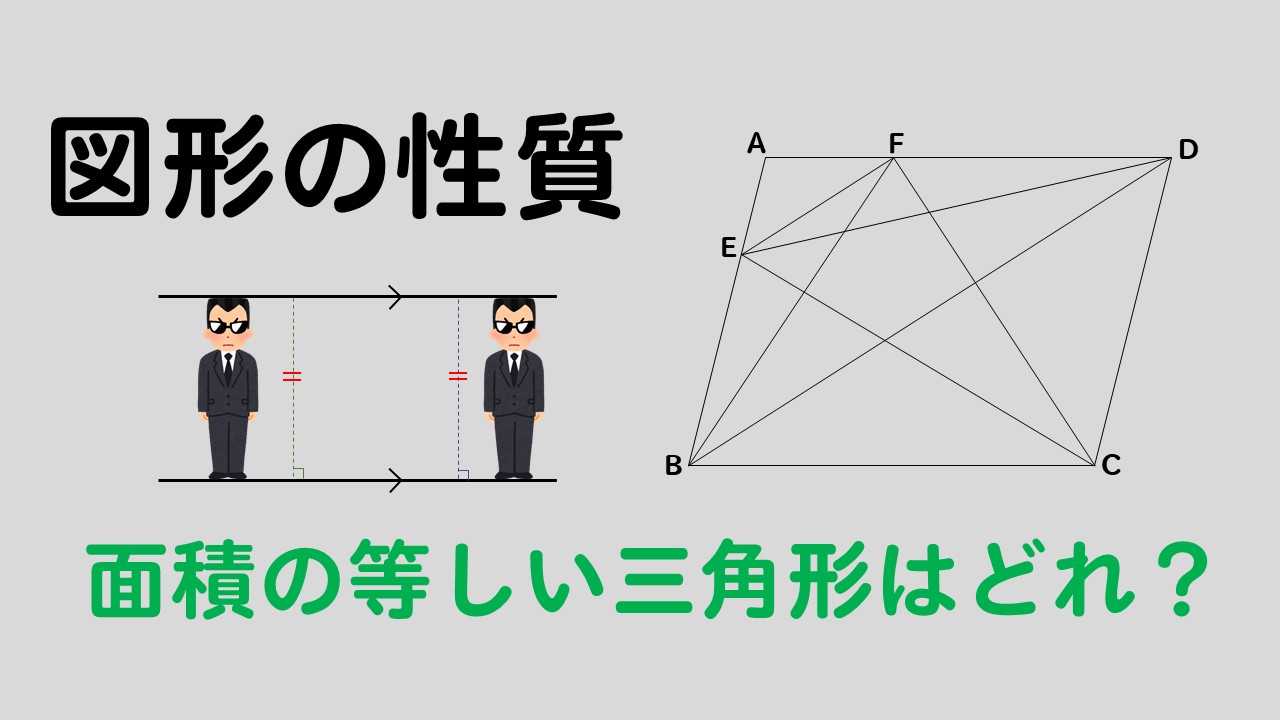



中2数学 平行四辺形の中から面積の等しい三角形を見つける問題を解説 数スタ
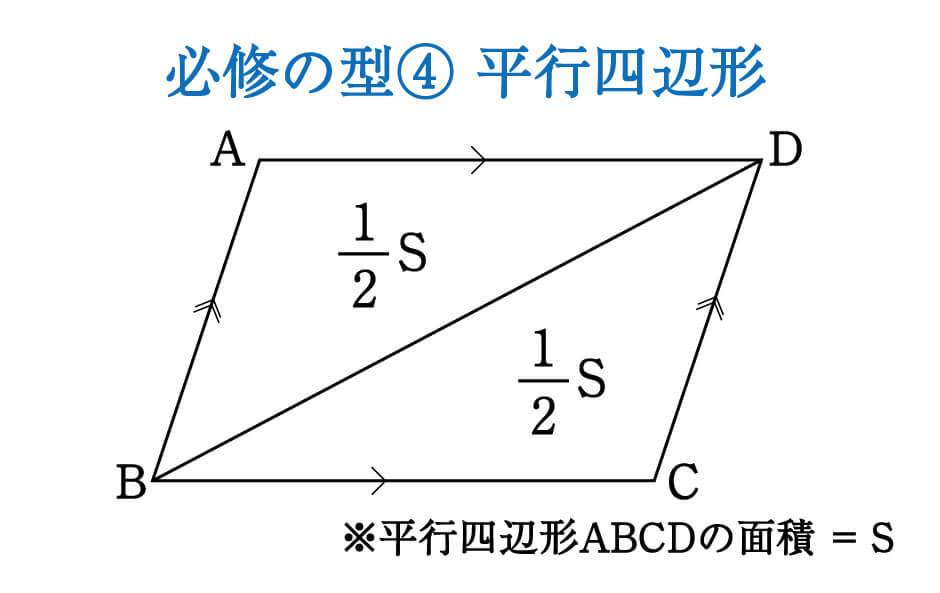



数学 面積比は全体から攻めると求めやすい 面積比 集中特訓 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo



平行四辺形全体の面積の何倍 大阪星光学院中学 2015 これが中学入試に出た図形問題
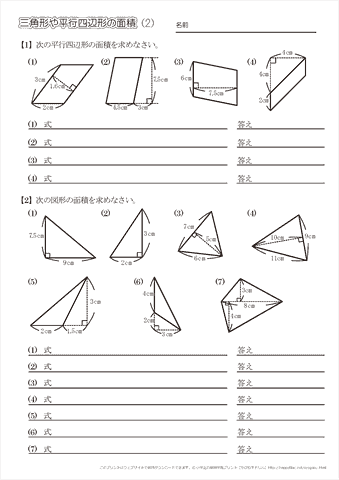



小学5年生の算数 三角形や平行四辺形の面積 問題プリント ちびむすドリル 小学生




1ヶ所に寄せ集めて求める面積問題 恋する中高一貫校 適性検査 徹底攻略



平面図形と比 平行四辺形の面積比 Next Stageのブログ
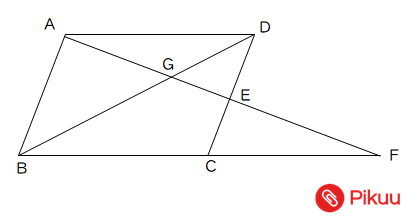



高校入試対策数学 面積比に関する対策問題 Pikuu
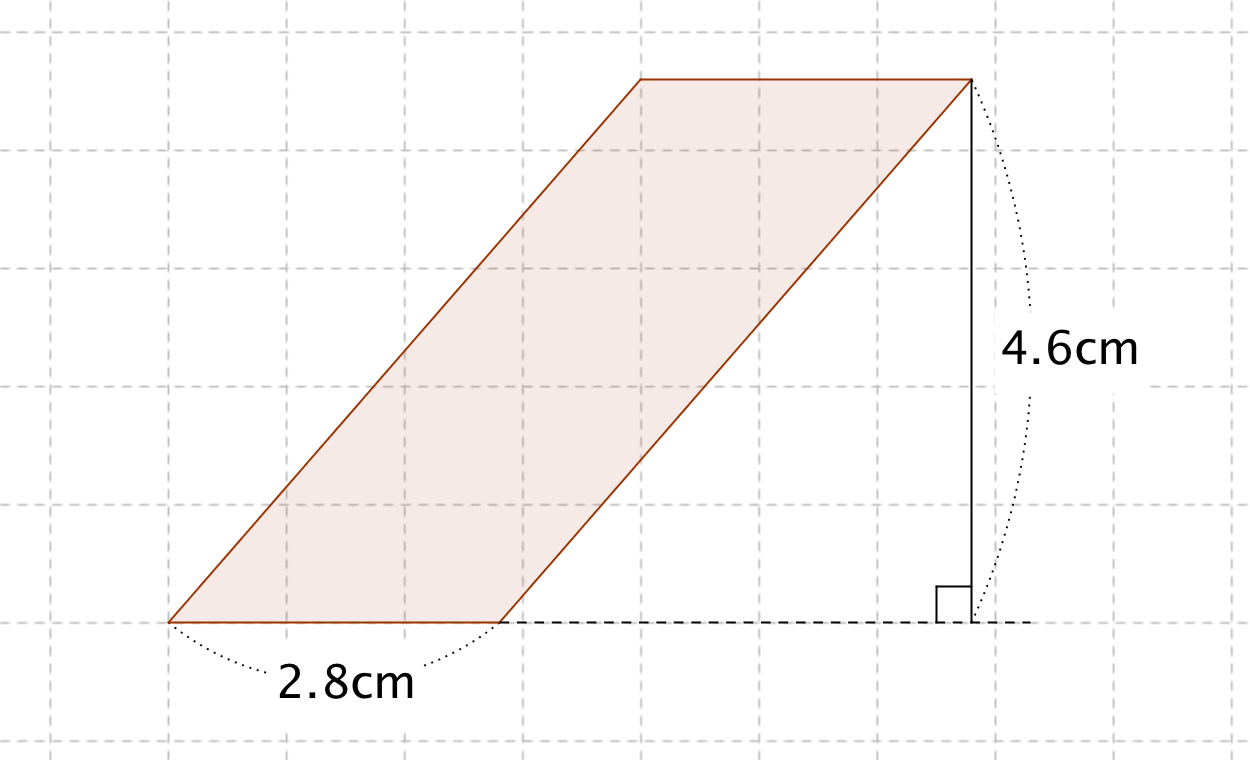



平行四辺形の面積の公式 算数の公式
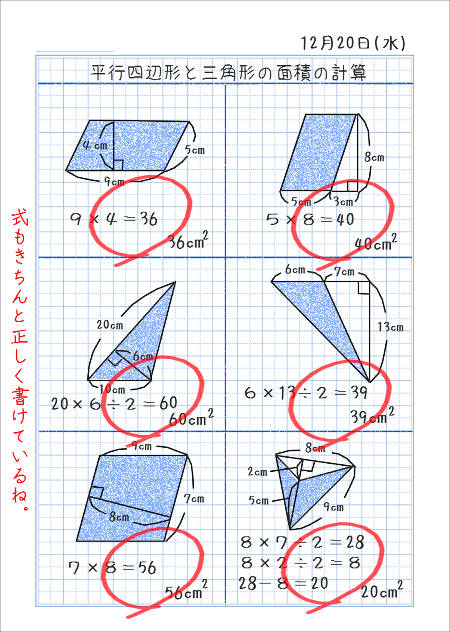



平行四辺形と三角形の面積 家庭学習レシピ




平行四辺形の面積の求め方 公式と計算例
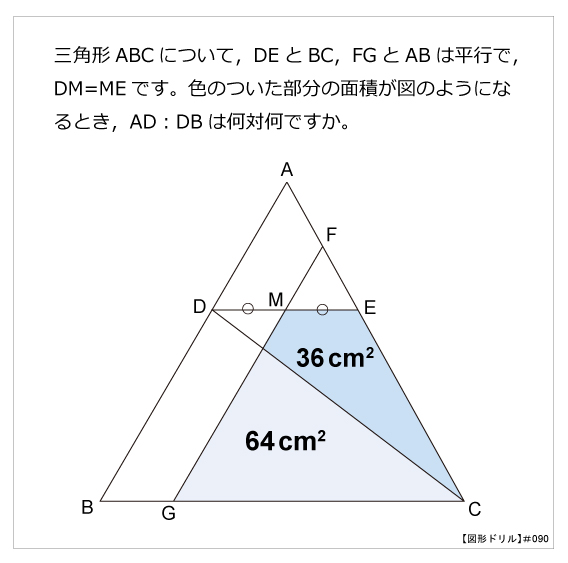



第90問 台形と平行四辺形 図形ドリル 第90問 台形と平行四辺形 算数星人のweb問題集 中学受験算数の問題に挑戦
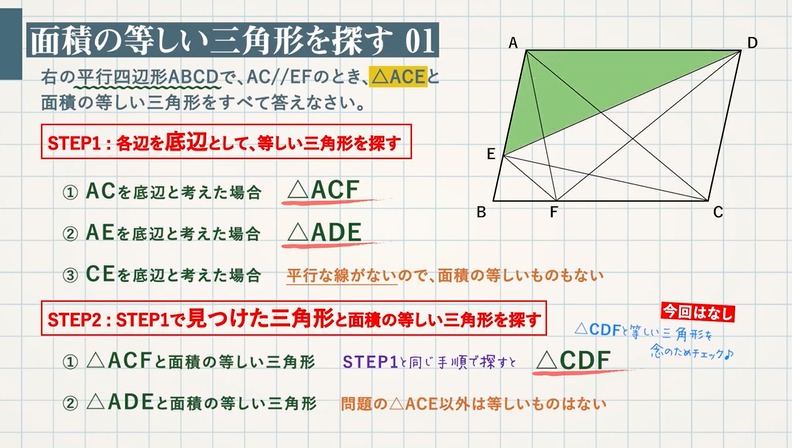



等積変形 面積が等しい三角形を探す 平行四辺形編 教遊者
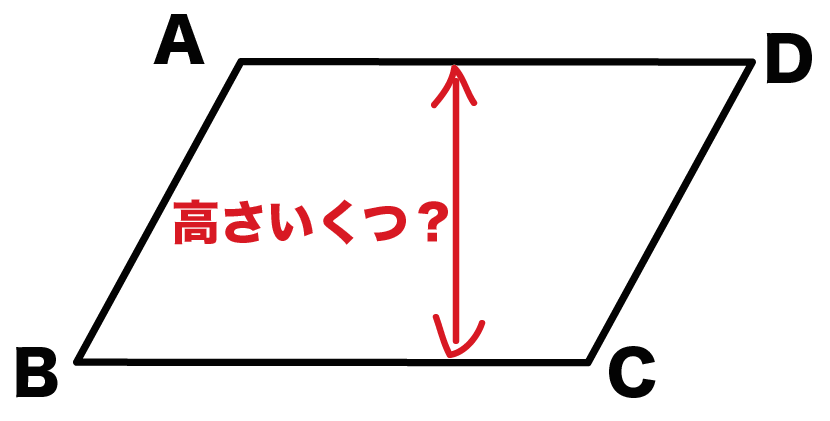



中学数学 平行四辺形の高さの2つの求め方 Qikeru 学びを楽しくわかりやすく




相似 平行四辺形と面積比の問題を徹底解説 数スタ



子どもを混乱させる相似な三角形の2つの面積比 算数数学が苦手な子専門のプロ家庭教師みかん先生
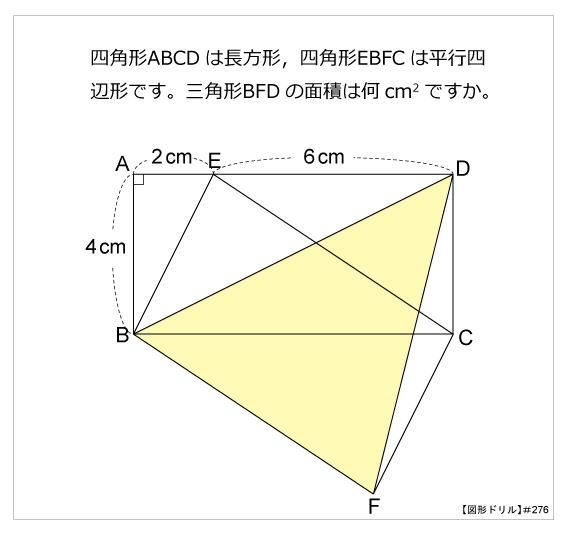



第276問 長方形と平行四辺形 図形ドリル 第276問 長方形と平行四辺形 算数星人のweb問題集 中学受験算数の問題に挑戦




面白い数学の問題 平行四辺形の中の三角形 平行四辺形って覚えてますか そらの暇つぶしch



2乗に比例 平行四辺形の面積 中学数学の無料オンライン学習サイトchu Su
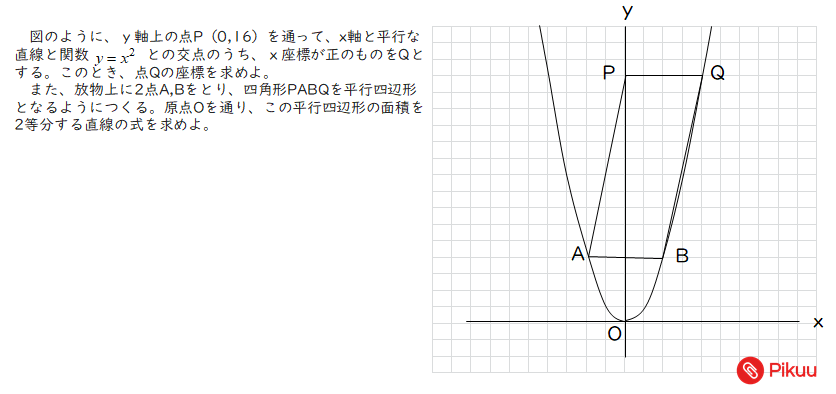



中学数学 平行四辺形の面積を二等分する直線を求める定期テスト予想問題 Pikuu




ベクトルの外積と平行四辺形の面積 身勝手な主張
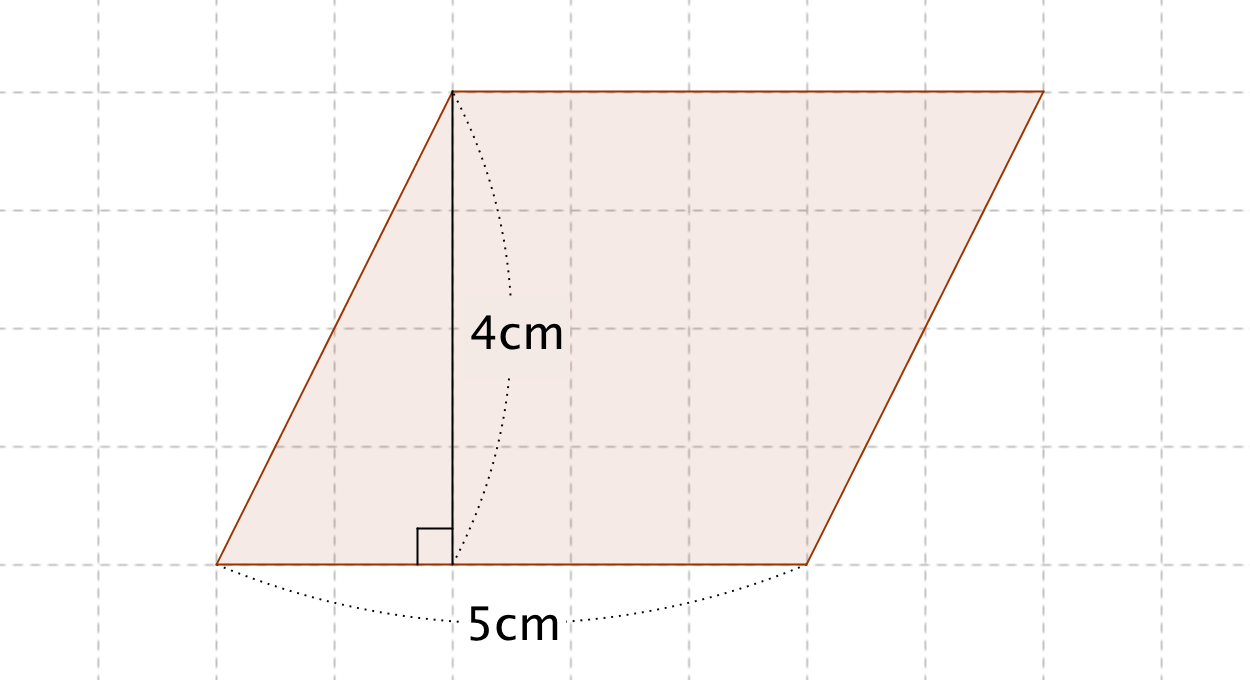



平行四辺形の面積の公式 算数の公式
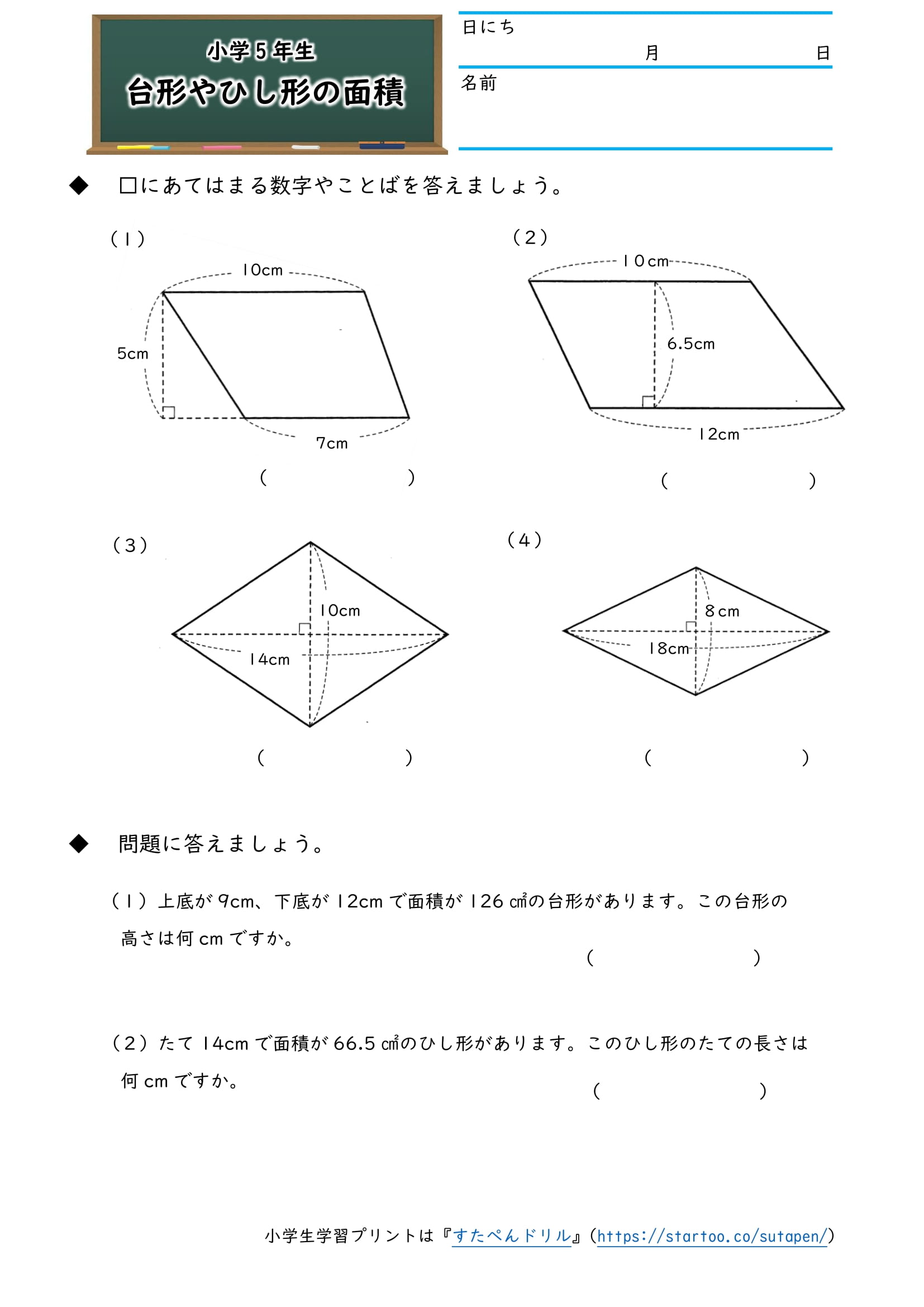



小5算数 四角形と三角形の面積 の学習プリント 練習問題 無料ダウンロード 印刷
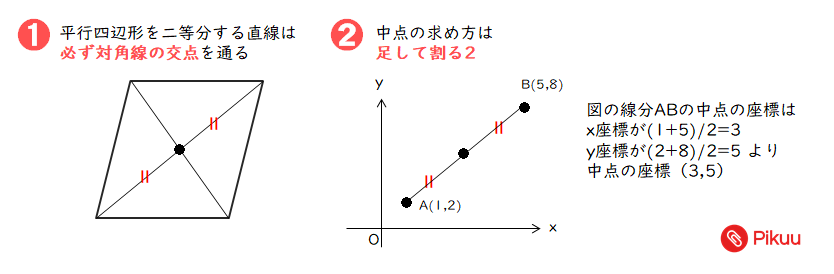



中学数学 平行四辺形の面積を二等分する直線を求める定期テスト予想問題 Pikuu



平行四辺形の面積の求め方で習う公式は なぜ底辺 高さになるの みけねこ小学校



平行四辺形の定義や性質を解説 面積の公式 証明問題も 受験辞典




小5 算数 小5 41 平行四辺形の面積 Youtube
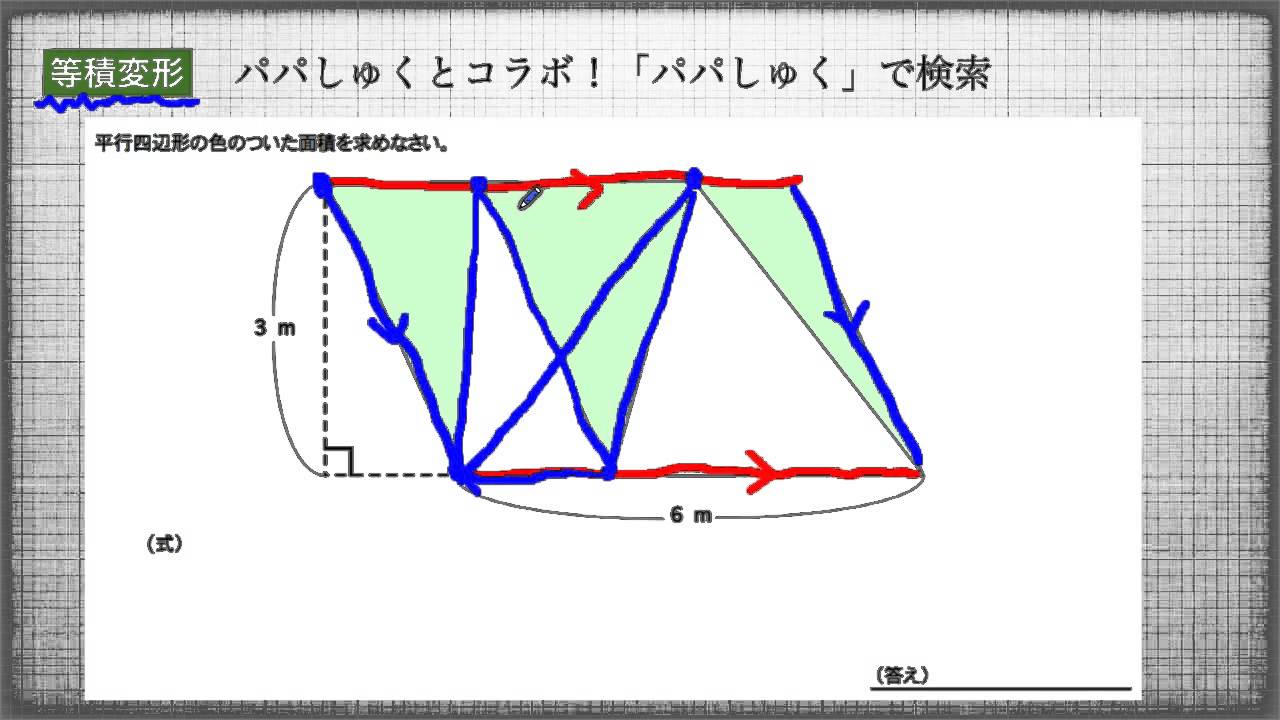



小学校5年 算数 面積 等積変形 問題編 パパしゅくとコラボしたよ Youtube
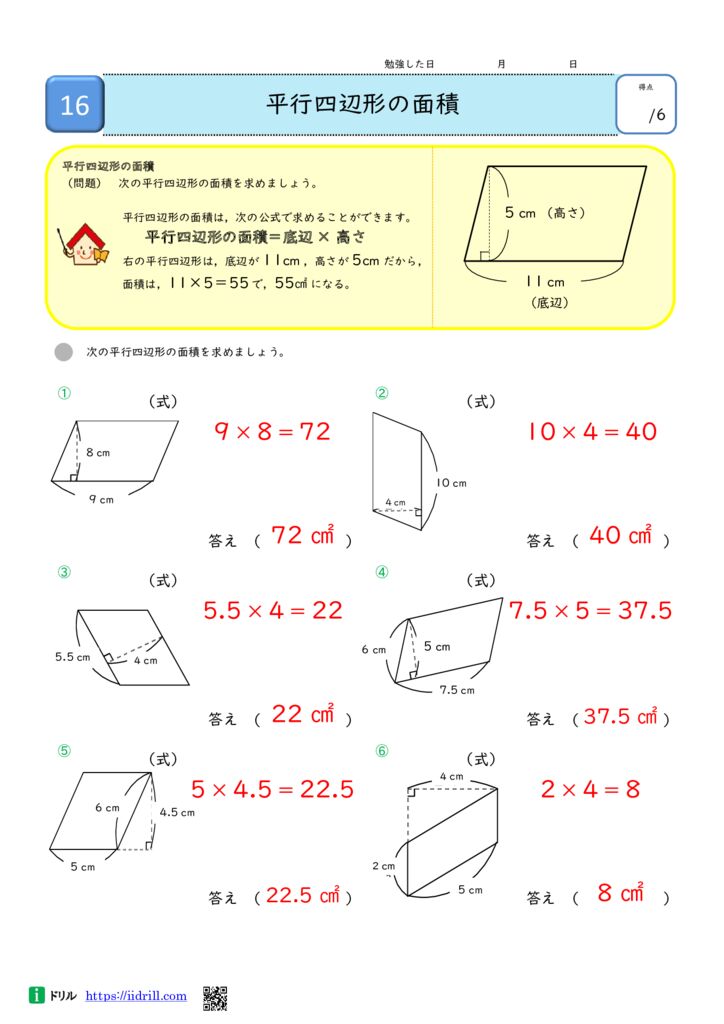



5年生算数ドリル 面積
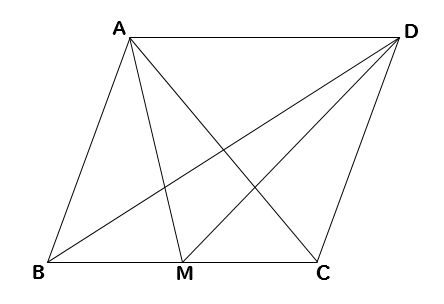



中2数学 平行四辺形の中から面積の等しい三角形を見つける問題を解説 数スタ




関数 グラフ上の平行四辺形の座標 面積 二等分線などの問題を解説 数スタ
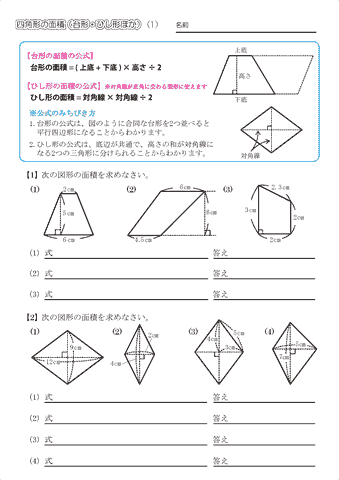



小学5年生の算数 四角形の面積 台形 ひし形ほか 問題プリント ちびむすドリル 小学生
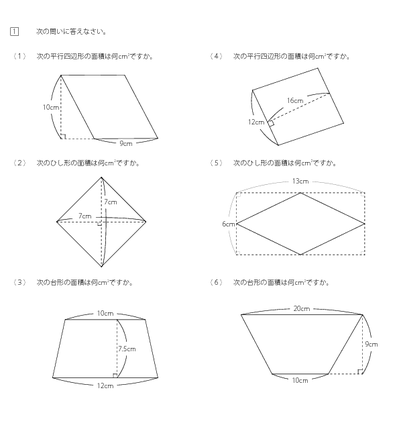



みんなの算数オンライン 教科書 平行四辺形 ひし形 台形の面積



平行四辺形の面積の何倍 今年 2018年 鎌倉学園中学 どう解く 中学受験算数



0 件のコメント:
コメントを投稿