中1では累積度数が新たに導入、資料の活用単元で多くの中1生を悩ませてきた(?)誤差、近似値、a×10 n は中3に移動となりました。 中2では四分位範囲と箱ひげ図が導入されます。 素数 中3社会は「公民―情報化やグローバル化」を教えました。中3数学は「近似値と有効数字」を教えました。 さて、Aさんは、長方形の縦と横の長さを定規で測りました。 縦が 372 cm で、横が 697 cm になりました。 掛け算で面積を出すと、 縦×横 =372×697 =2584 となりました。平方根の近似値 解説 平方根を含む数の大小比較は,小数の近似値を使えば簡単にできます. 例 √2= で √7= だから √2+√7= √3=173 で √6= だから √3+√6= したがって √2+√7 < √3+√6 が言えます. 問題 下の2つの数のうち大きい方を選びなさい

中1数学 近似値と誤差のポイントと練習問題 中学生勉強サイトあかね先生
近似値 中3
近似値 中3-今回は中3で学習する平方根の単元を扱っていきます。 ひとよひとよにひとみごろ~ 一方で、語呂合わせでちゃんと近似値を覚えておけば $$\Large{3(\sqrt{2}\sqrt{3})}$$ $$\Large{≒ 3()}$$ $$\Large{=3314近似値 近似値とは 真の値に対して、真の値ではないがそれに近い値を近似値という。 測定値や四捨五入して得られた数字は近似値である。 誤差 近似値と真の値の差を誤差という。 誤差=近似値ー真の値
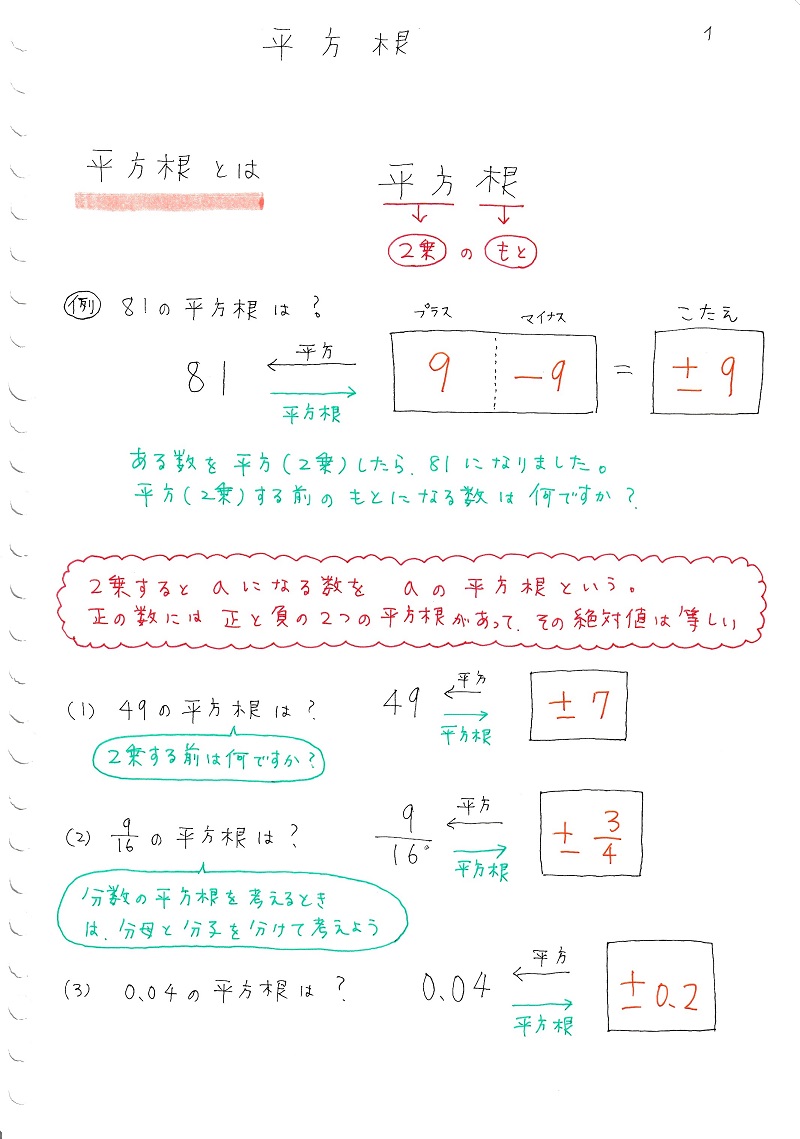



中学数学 平方根 ママ塾ノート
誤差と有効数字、近似値の表し方の問題です。高校の理科でも使う分野なので、教科書でしっかり意味を確認してから問題に取り組んでください。誤差とは、真の値と近似値との間にある違い、つまり、誤差=近似値-真の値です。例)測定値 505kg 真の値 502kg のとき 505kgー502kg=03kgが誤差になる。よく出る問題ある数aの小数第二位を四捨五入すると 32@ @ 3=173 @ Ł@ 6= @ @ 3 { 6= @ @ ā@ 2 { 7 @ @ 3 { 6 @ ܂ D 以下の選択肢から最も近い値を選んでください。 — Lillian (@Lily0727K) 19年5月10日 コイン投げ まずは簡単な場合でコインを4回投げた場合を計算してみます。 表が出る回数 確率;
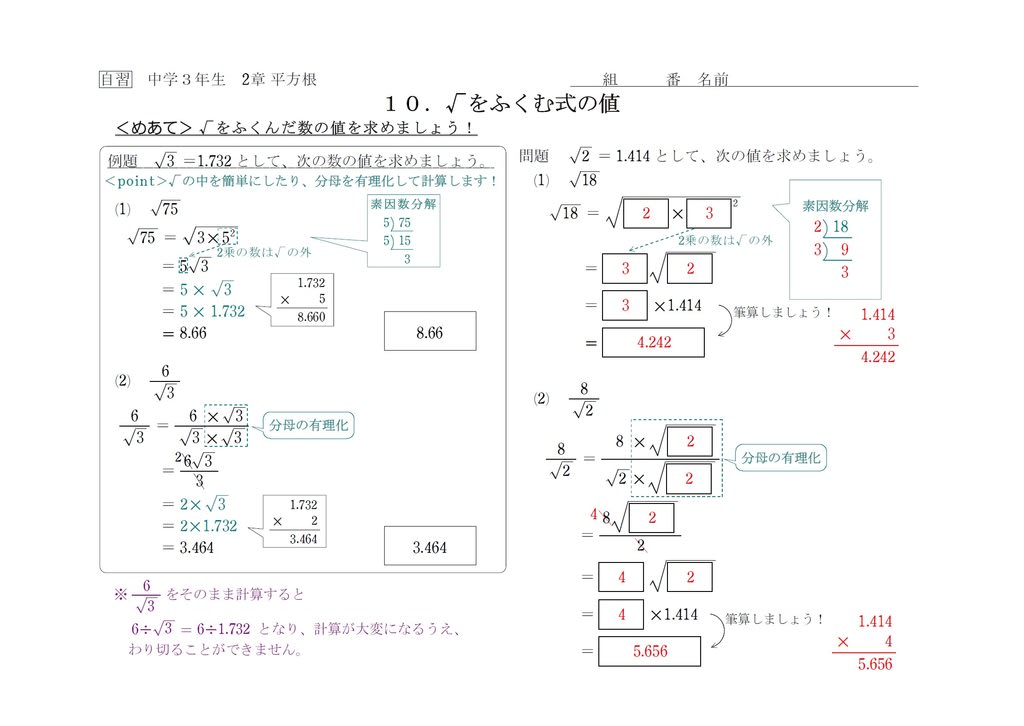
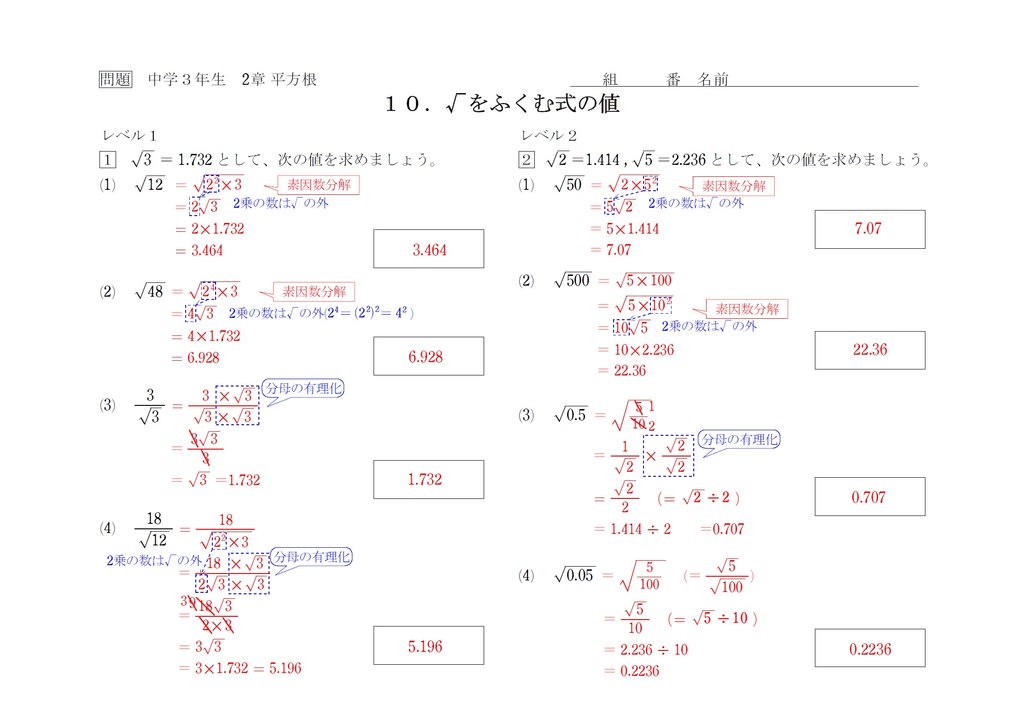
教科書 新編 新しい数学3 東京書籍, 単元 平方根,根号をふくむ式の計算, 「語呂合わせでの覚え方のまとめです! よかったらこれで覚えてみてくださーい!」, 学年 中学3年生, キーワード 平方根,近似値,素数,暗記 平方根の近似値の考え方と、平方根の表から近似値を求める問題です。 *時間があれば電卓を使って確認してみてください。 近似値2 式を変形して近似値を求める問題です。 よく出題されるのでパターンを覚えてください。 くもんの中学基礎がため100%中3数学 計算・関数編―学習指導要 近似値 長さと重さなどを測定して得られた値や四捨五入して得られた概数などのような、真の値に近い値 を近似値といいます。 誤差 近似値から真の値をひいた差を誤差といいます。
近似値 きんじち approximate value 真の値すなわち正しい値そのものが算出できないとき,あるいは算出できてもそれほど精密な値を必要としない場合に,その代りとして使用される,真の値に近い数値のことを,近似値という。 たとえば は円周率 π の近似値,2718は自然対数の底 e の近似近似値 たとえば (※ なお、もし中1で習わなくても、中学3年の別の単元で、表計算ソフトなどの活用を習う。中学3年で、どの教科書会社でもコンピュータを使った、統計の分野の手法を習う。) 上述の計算例では、人間の手でも計算しやすいていどに、度数などを減らしているが、実際の2次の近似式 (5)式は h が 0 に十分近いとき h の1次式で近似式を表わしたものとなっている f(ah)≒f(a)f'(a)h ・・・(5) 目的に応じてさらに詳しい近似式がほしいときは, h の2次式,3次式,・・・と次数を高くしていくとより精度の高い近似式が得られる.




高校数学 近似値 平方根 円周率 常用対数 自然対数の底 のゴロ合わせ 受験の月




平方根とは 東大生が平方根の計算方法や覚え方を伝授 高校生向け受験応援メディア 受験のミカタ
0回 1/16 1回 4/16 2回 6/16 3回 4/16 4回 1/16 例えば4回中2回が表になる確率は以下のように求められます。 _4\rm C_2Subscribe 中3 数学 平方根12 近似値を使う計算 (4分) Info Shopping Tap to unmute If playback doesn't begin shortly, try restarting your device You're signed out Videos you watch may be added to the TV's watch history and influence TV recommendations To avoid this, cancel and sign in to on your computer ルートの近似値と覚え方 2 ≒ \sqrt {2}\fallingdotseq 2 ≒ (一夜一夜に人見頃) 語呂の意味はよく分かりませんが,非常に有名です。 3 ≒ \sqrt {3}\fallingdotseq 3



中学校1年生数学 近似値 長野地区 Itto個別指導学院 長野市の学習塾
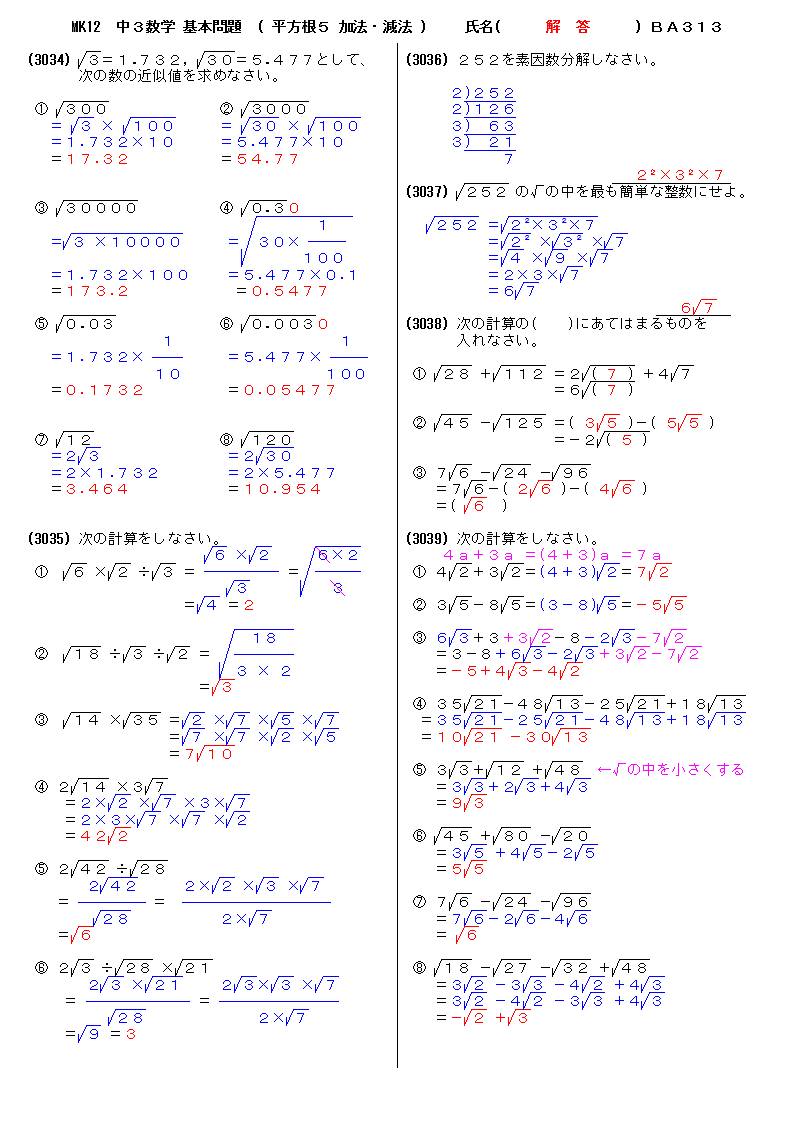



無料 中3数学 基本問題 解答プリント 313 平方根5 加法 減法
近似値の求め方はあとで解説しますが、√2、√3などのよく出てくる平方根は、近似値は覚えてしまったほうが答えの確認などに使えて便利です。だいたい少数第2位まで覚えておけば十分でしょう。 √2 ≒ 141 √3 ≒ 173 √5 ≒ 224 √7 ≒ 264 √3=1732のときAbout Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features © 21 Google LLC手計算によるルートの解法は、以下に挙げる3通りの方法が考えられるが、平方根の解法は、どれか一つの方法を使うと言うよりは、問題の形式(ルート中の数字)に合わせて使い分けることが大切である。また、手計算は「慣れ」であるため、普段から練習する事が大切である。 1 近似値法 2




中3数学 平方根 ルートの値を語呂合わせ 覚え方まとめ 数スタ




中学数学 近似値 有効数字 から誤差を求める1つの方法 Qikeru 学びを楽しくわかりやすく
無料 中1数学 基本解説 問題プリント 資料の活用2 近似値 テキスト 中1数学の学習プリントのPDFファイル 中1数学の学習プリントはPDFファイルで項目別にまとめてダウンロードできます。 全て、問題プリントと解答プリントのセットです。(ヒントページはありません) 中1数学の学習プリント中3です。「平方根」の近似値を使う問題が。 中学生から、こんなご相談が届きました。 「 平方根の近似値について、 使い方がよく分かりません。 "√2=1414""√=4472 "を、どう使うのですか?」 なるほど、 「これを使いなさい」と近似値が3.指数近似 (x,y)の点群データから、指数関数による近似曲線を求めます。 図3-1 指数近似曲線 y=a exp(bx)=a e bx Excelで求める値は、指数関数の係数であるaとxの係数であるbになります。
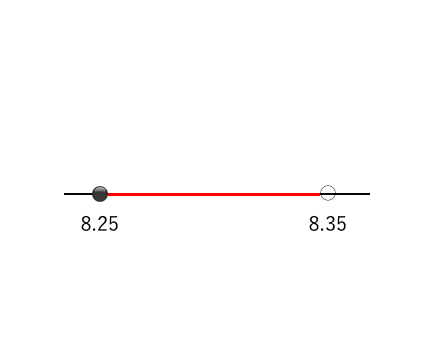



近似値の問題 苦手な数学を簡単に




中3数学 平方根の近似値 Youtube
「中3への移行、大賛成!」 という気持ちでした。 簡単に言えば、 「 近似値とはおよその値で、 有効数字とは、そのおよその値のうちの 信用していい部分の数字 」 という説明になりますが、 中1の生徒たちには、 「???」となりやすかったわけですね。 近似値の求め方で √の中が小数の場合どのように求めるのですか? また、分数の場合はどう求めるのでしょうか。 3√10/5はどうなりますか。 質問多くてごめんなさい。 お願いします 数学 数3微分法の応用です。 sin31°の近似値を,1次の近似値を用いて,小数第3位まで求めよ。ただし,π=3入試数学コンテスト 2 sin30°の値が2分の1になるのはどうしてですか?求め方も教えていただけますでしょうか。 3 解法の最初の2行が成立する理由を教えてください(東大文122)




中3数学 平方根の近似値 映像授業のtry It トライイット



1
一致か近似値かの値は、1か0か1を指定します。 0が基本で、検索値と全く同一のものを探す場合で、1または1の場合、近似値を探します。 ☆注意:近似値の場合は、あらかじめ一覧の範囲を並べ替えておかなければなりません。 1では昇順:範囲の中の近似 可変の配列に数値が格納されており、指定した値がその配列の中の数値と等しいものが見つからない場合に、近似値を返す。 例: 数値群{8,9,10,14,16,} 10を指定した場合は10が返る 11を指定した場合は10が返る 平方根の近似値を求める問題です。 おおよその値を知ることは、具体的に想像しやすくなるということ。とても大事です。 平方根の近似値(およその値) 平方根の近似値(およその値) 答えつき Tweet 登録カテゴリ 1030中3 数学




中学数学 近似値 有効数字 から誤差を求める1つの方法 Qikeru 学びを楽しくわかりやすく



中3 根号の近似値 の教え方 塾講師 数学マンは踊る
平方根の「近似値」 中3生の「数学」のコツ 中3です。 「平方根の近似値」、応用問題が。 中学生から、こんなご質問が届きました。 近似値の求め方が分かりません」 平方根の 「近似値」 の問題ですね。 大丈夫、コツがあるんですよ。 近似値を求められるんです。 以下で解説していきますね 中3「根号の近似値」の教え方 カテゴリー 中学数学 (21) 北辰 (6) 教え方の一般論 (3) 高校受験 (1) 月別アーカイブ はてなブログをはじめよう! sugakumanさんは、はてなブログを使っています。あなたもはてなブログをはじめてみませんか? はてなブログをはじめる(無料) はてなブログπ の近似値 このページでは過去発表された円周率の近似値を表す数式を紹介する。 元の表記方法(の日本語訳)をそのままを使うと(特に古い文献で) 円周率を求めた記述ではないというような解釈ができるが ここでは π = π = の形に解釈したものを




ルート3の近似値の求め方4パターン 数学の星
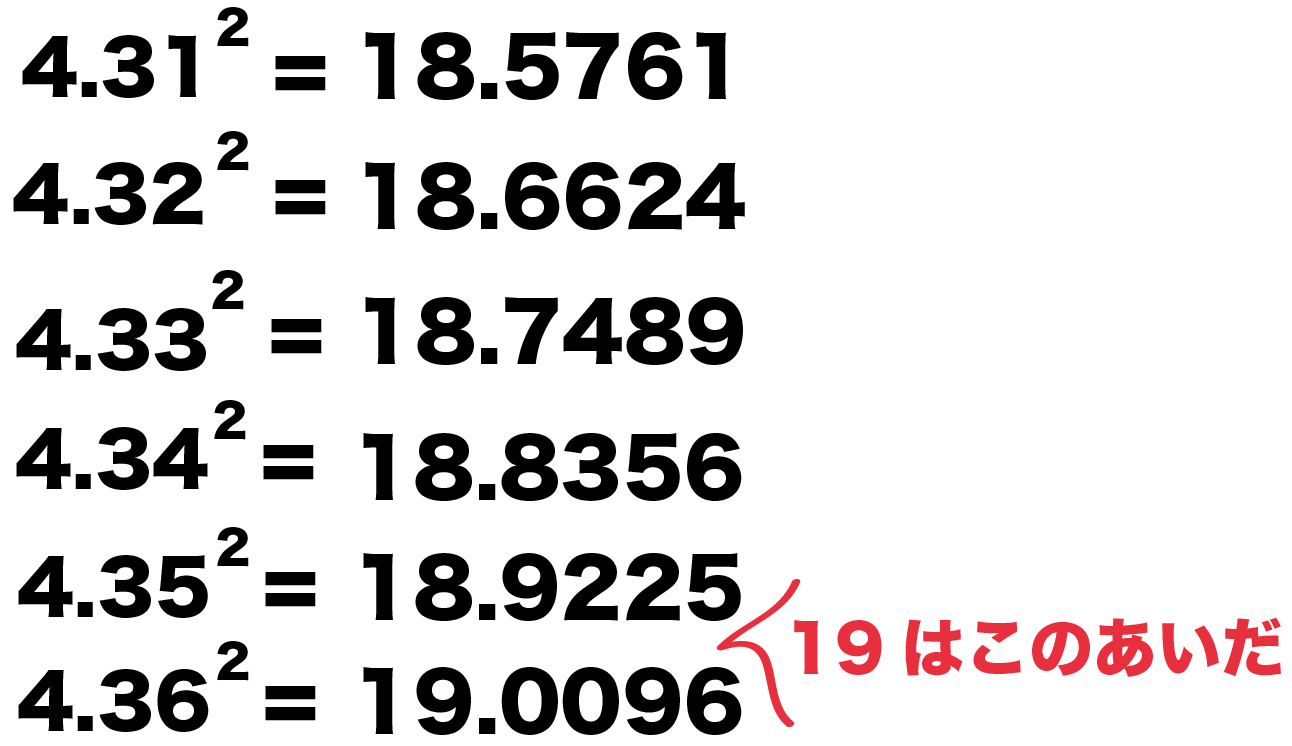



中学数学 3分でわかる 平方根の近似値の求め方 Qikeru 学びを楽しくわかりやすく
近似一致を使って、列 a で値 1 を検索し、列 a で 1 以下の最大値である 0946 を見つけて、同じ行の列 b の値を返します。 217 =vlookup(1,a2c10,3,true) 近似一致を使って、列 a で値 1 を検索し、列 a で 1 以下の最大値である 0946 を見つけて、同じ行の列 c の値を返します。 100 =vlookup(07,a2c10,3,false




中1数学 近似値と誤差のポイントと練習問題 中学生勉強サイトあかね先生



中1数学 基本解説プリント 資料の活用2 近似値 問題 145



画像 ルート 展開 近似 ハイキュー ネタバレ



中3数学近似値 やり方があっているか不安なので教えてください 1 2 Yahoo 知恵袋




中3 数学 平方根12 近似値を使う計算 4分 Youtube




中3数学 平方根 18 中学数学高校数学個別指導in山形市 数専ゼミ




โน ตของ 資料の活用 標本調査 近似値と有効数字 ช น Junior Clear




中学1年生 数学 資料の活用 近似値と有効数字 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




中1 数学 中1 近似値 Youtube




中3 ルートの近似値の求め方をイチから解説 Youtube




中学応用 整数部分 小数部分の求め方 分数の場合には 数スタ




中学数学1年 代入と式の値 受験の月




中学数学 3分でわかる 平方根の近似値の求め方 Qikeru 学びを楽しくわかりやすく




中3数学 真の値と近似値の定期テスト過去問分析問題 Atstudier




平方根の近似値 無料で使える中学学習プリント




中3数学 平方根 19 中学数学高校数学個別指導in山形市 数専ゼミ




近似値と有効数字 教遊者




近似値と有効数字 中1から中3に移行した単元 校舎ブログ詳細 校舎検索結果詳細 校舎を探す 学習塾 個別指導塾 予備校の秀英予備校




中1数学 近似値と誤差の求め方の定期テスト予想問題 Pikuu




画像 ルート 展開 近似 ハイキュー ネタバレ




中学1年生 数学 資料の活用 近似値と有効数字 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



1




中3数学 平方根 近似値と有効数字 授業 Youtube




中学数学 平方根 整数になる自然数n の簡単なやり方 丁寧な解説 スタディーランナップ




中3数学 平方根の近似値 例題編 映像授業のtry It トライイット




Mer 新学習指導要領で理科と数学の関連を憂うのであれば むしろ現中1にある 誤差や近似値 A 10 Nの形 が中3 に飛ぶのは大丈夫なんですか 現行は 理科との関係で中1に入ったんじゃなかったでしたっけ こちらは特に話題になりませんでしたけど




中学数学 平方根 ママ塾ノート




中3数学2 11 平方根の近似値 Youtube



中3自習 平方根5 近似値 中学数学の勉強に




中学3年 数学 平方根 中学生 数学のノート Clear



Studydoctor ルートの近似値の求め方 中3数学 Studydoctor




中3数学 平方根の近似値の求め方 5分で学習 Youtube




近似値およその値 中3数学 平方根8 Youtube




近似値と有効値 数学の要点まとめ 練習問題一覧




高校数学 近似値の計算 問題編 映像授業のtry It トライイット




平方根で近似値の応用問題です はどうやって解きますか Clear




中学数学 平方根 のコツ 有理化 加減乗除 展開



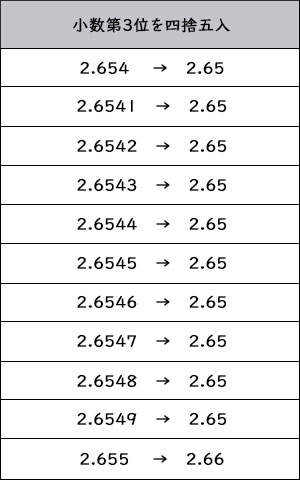
この写真の平方根表を使います 7 2が少数第3位を四捨五入すると 2 Yahoo 知恵袋




中学数学3年 いろいろな平方根の計算 平方根と式の値 受験の月




中3数学 平方根の近似値の問題です Clear



平方根の活用 式の値と近似値の求め方 教遊者



中3 平方根10 近似値 中学数学の勉強に




無料 中3数学 発展 応用問題 問題プリント 314 平方根6 いろいろな計算1



至急明日テストです 中三数学の近似値の問題です 3 の解き方って Yahoo 知恵袋




中3数学 平方根 近似値と有効数字 問題 Youtube




中3 数学 無料学習プリント教材



Www Pref Osaka Lg Jp Attach 6629 Jmw 1d7 5 Pdf




中1数学 有効数字 近似値と誤差の要点と定期テスト対策問題 Examee




中1数学 近似値 練習編 映像授業のtry It トライイット



1



中3数学です 次の数の近似値を 平方根表を使って 小数第3位ま Yahoo 知恵袋



平方根まとめ




中3 平方根10 近似値 中学数学の勉強に




中3数学 平方根の近似値の問題です Clear




数学 近似値 中学生 数学のノート Clear




中学数学 平方根 のコツ 平方根の近似値 式の値




中3 平方根10 近似値 中学数学の勉強に




中学数学 平方根 のコツ 平方根の近似値 式の値




中3 数学 平方根の利用 この問題の解説をお願いします 整数部分と少数 Okwave



至急お願いします中学数学で 近似値計算 測定値 などの言葉が出てくる単 Yahoo 知恵袋



1



興坪だより 中2 中3の数学 かなり ほぼ理解した喜多郎 日本の中学数学が遅すぎる
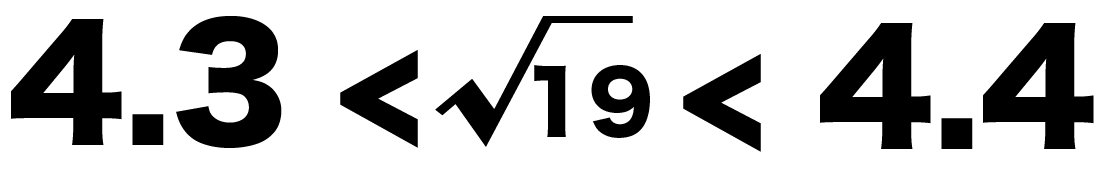



中学数学 3分でわかる 平方根の近似値の求め方 Qikeru 学びを楽しくわかりやすく




平方根の近似値を語呂合わせで覚える わさん先生のうわごと




中3数学 近似値を使う計算 練習編 映像授業のtry It トライイット




中1数学 近似値 映像授業のtry It トライイット
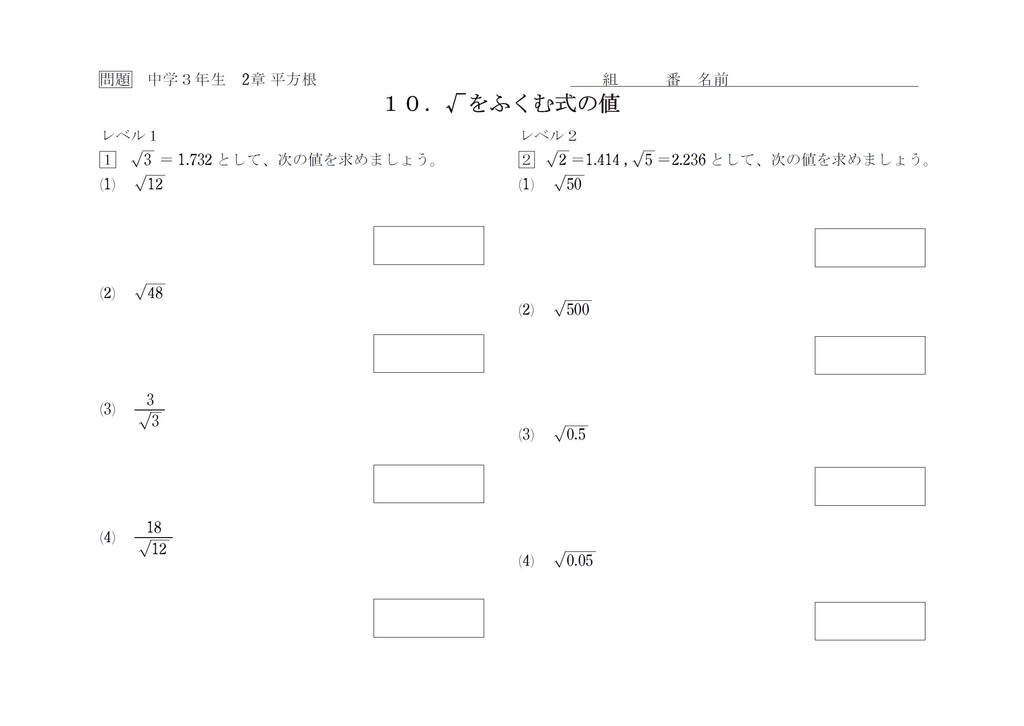



中3 平方根10 近似値 中学数学の勉強に




中学3年 数学 平方根 中学生 数学のノート Clear




中学1年生 数学 資料の活用 近似値と有効数字 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
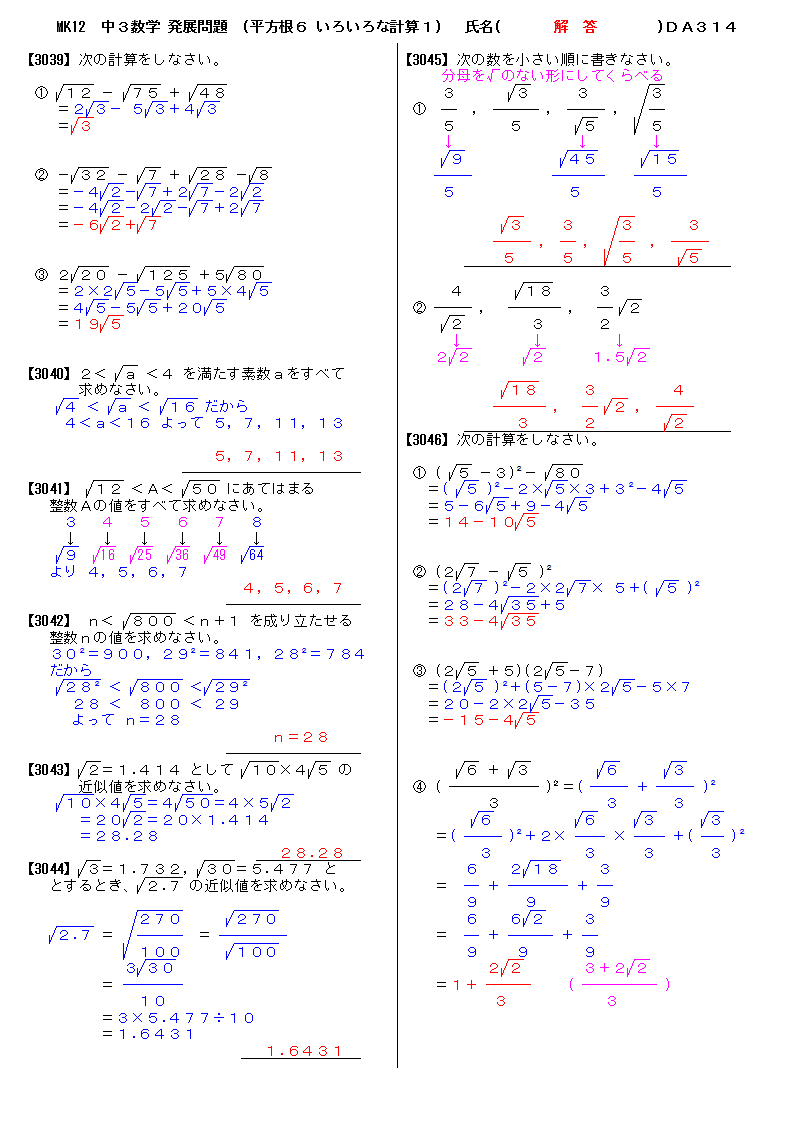



無料 中3数学 発展 応用問題 解答プリント 314 平方根6 いろいろな計算1




平方根の近似値 無料で使える中学学習プリント




中3数学 平方根の近似値 練習編 映像授業のtry It トライイット




中3数学 真の値と近似値の定期テスト過去問分析問題 Atstudier




近似値と有効値 数学の要点まとめ 練習問題一覧
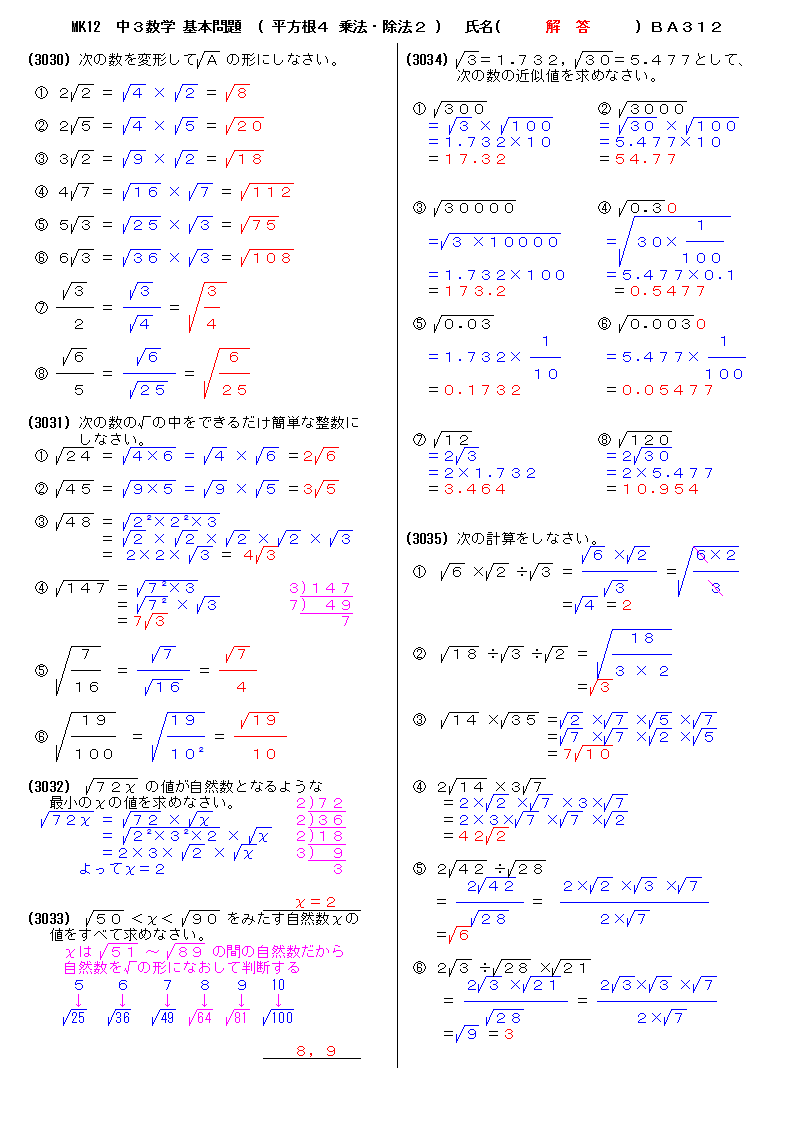



無料 中3数学 基本問題 解答プリント 312 平方根4 乗法 除法2




中3数学 平方根の近似値 練習編 映像授業のtry It トライイット




中3数学 近似値を使う計算 練習編 映像授業のtry It トライイット




画像 ルート 展開 近似 ハイキュー ネタバレ




平方根の近似値 無料で使える中学学習プリント



中3第2章1 平方根10 平方根の近似値 プログラミングの雫




平方根 清水塾




無料 中3数学 発展 応用問題 問題プリント 313 平方根5 加法 減法




平方根の近似値 無料で使える中学学習プリント




中3 数学 無料学習プリント教材
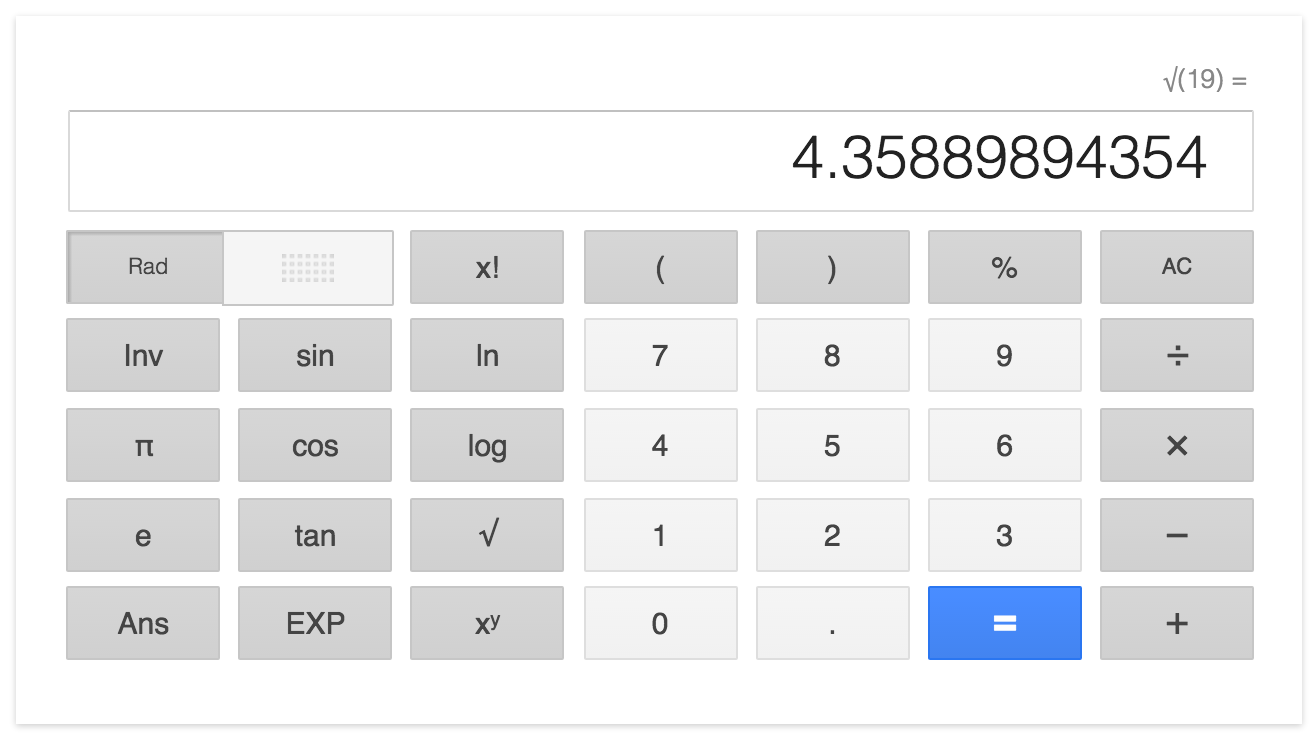



中学数学 3分でわかる 平方根の近似値の求め方 Qikeru 学びを楽しくわかりやすく
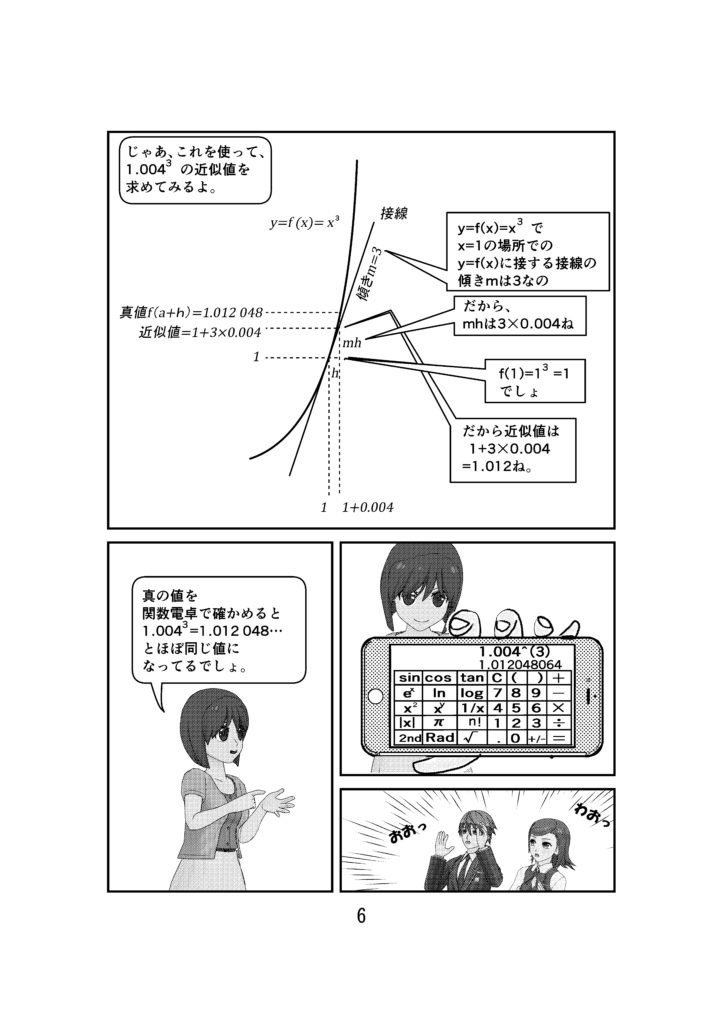



イメージでわかる冴子先生の高校数学 近似式編 数学はこちら 漫画で表してます Manabi100




画像 ルート 展開 近似 ハイキュー ネタバレ




無料 中3数学 発展 応用問題 解答プリント 312 平方根4 乗法 除法2
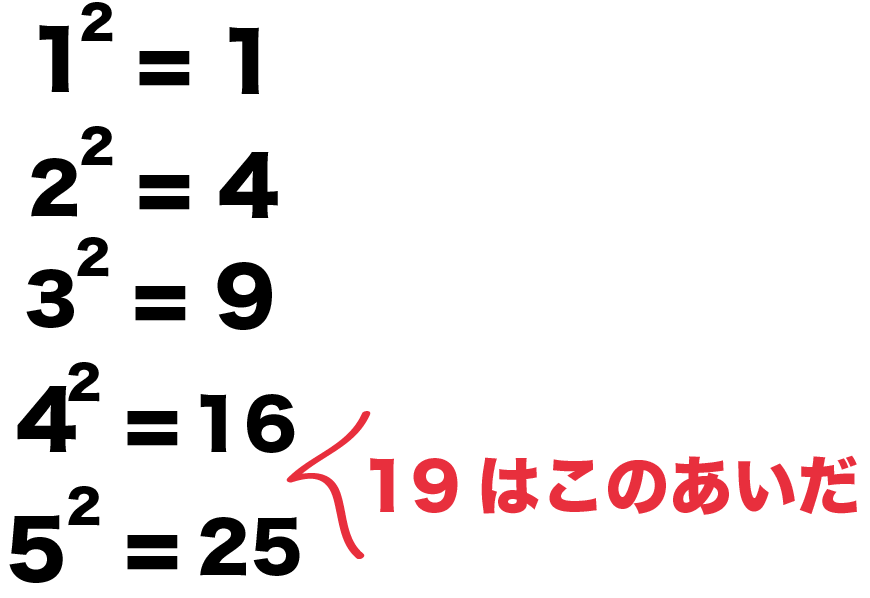



中学数学 3分でわかる 平方根の近似値の求め方 Qikeru 学びを楽しくわかりやすく




画像 ルート 展開 近似 ハイキュー ネタバレ



0 件のコメント:
コメントを投稿