1 単元名「三角形」 2 単元の目標 二等辺三角形や正三角形の性質や美しさに関心をもち,身の回りからそれらの形をさがそうとする。 (関心・意欲・態度) 辺の長さや角の大きさに着目して,三角形の性質などを考える。 (数学的な考え方)算数 算数5年/三角形の角の大きさ① ラーニング 1 《1.三角形の角の大きさ》 どんな三角形でも,3つの角の和は180°です。 角ア+角イ+角ウ=180° 下の図の三角形で,ア,イの角度を求めなさい角とその大きさ 分度器 解説 分度器ペンつき 解説 分度器角度扇の色つき 解説 2度の測り方 解説 340度の測り方 解説 角の大きさ 解説 角とその大きさ 解説 さまざまな三角形 解説 三角形の内角の和 解説 もとのかずはいくつ 解説 広さを

三角形の角度を求める問題 小学生 中学生の勉強
三角形の角の大きさ
三角形の角の大きさ-年 組 番 名前 591 図形の角 三角形の角の大きさ 1 2 3 4 5 三角形の3つの角の大きさの和は 度です。三角形に分けられます。三角形の角の大きさの和は なので,五角形の5つの角の大きさの和は, になります。 三角形の3つの角の大きさの和を調べましょう。 三角形や四角形の角 三角形の角 名 前 133〜138ページ) 四角形や五角形の角の大きさの和を調べ




図形の調べ方 三角形 役に立つ角度の求め方 苦手な数学を簡単に
見積りにて三角形の角度を出したかったのですが、計算式なんて忘れてますよね~(><;)非常に助かりました! ありがとう~! 0001三角形についての観察や構成などの活動を 通して,三角形を構成する要素に着目し,二等 辺三角形や正三角形,角について理解する。 イ 単元計画 単元計画(表2)を作成した。 辺三角形の作図の仕方を考える。 表2 単元計画 形を作り,辺の長さが等しいこ③ 三角形,四角形,五角形,のように直線で囲まれた図形を と いいます。 多角形の角の大きさの和について考えましょう。 (3)多角形の辺の数と,角の大きさの和を表にまとめましょう。
求角と方程式 角度を求めることは、小学生のころにもやっていることです。 しかし、角度を求めるために方程式を用いることは中学生ならではです。 そんな問題を練習しましょう。 例題1 次の図の角 \(x\) の大きさを求めなさ算数 5年算数/三角形の角の大きさ ラーニング 1 どんな三角形でも,3つの角の和は180°です。 角ア+角イ+角ウ=180° 《1三角形の角の大きさ》 例題1 解答 下の図の三角形で,ア,イの角度を求めな二等辺三角形や正三角形の定義や性質を生かして,コンパスを用いて作図することができる。 (技能) 二等辺三角形や正三角形の定義や性質,角の意味について理解できる。 (知識・理解) 3 指導にあたって 〈単元の前後関係〉 1年
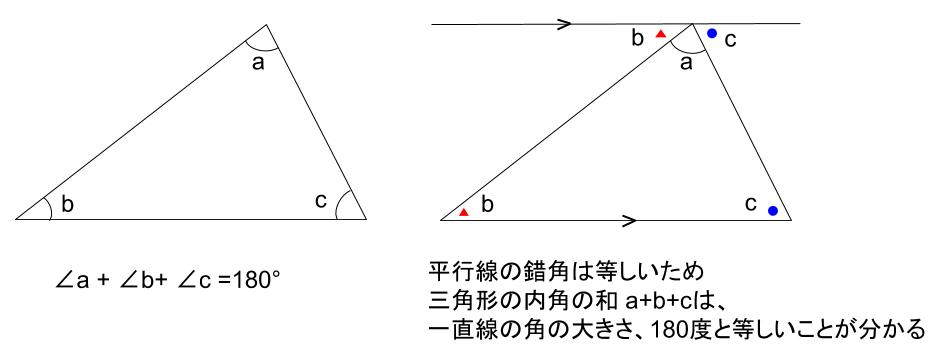
(3)2つの角が等しい三角形は、二等辺三角形である。 逆 二等辺三角形は、2つの角が等しい。 (4)合同な図形の面積は等しい。 逆 面積が等しい図形は合同である。 × (5)6の倍数は偶数である。 逆 偶数は6の倍数である。 × (例)2三角形の内角と外角の性質は次の $2$ つとなります。 ① 三角形の内角の和は $\textcolor{blue}{180°}$ である ② 三角形の外角は、それととなり合わない $\textcolor{blue}{2}$ つの内角の和に等しい まずは、① 三角形の内角の和は $180°$ である について、なぜそうなるのか確認答え 二等辺三角形が2つくっついている問題ですね。 この場合、それぞれの二等辺三角形に注目して角度を1つずつ求めていきます。 赤い二等辺三角形は、頂角が36°なので 底角1つ分の角は となります。 そこから、次は青い二等辺三角形に注目して を



内接円 内心
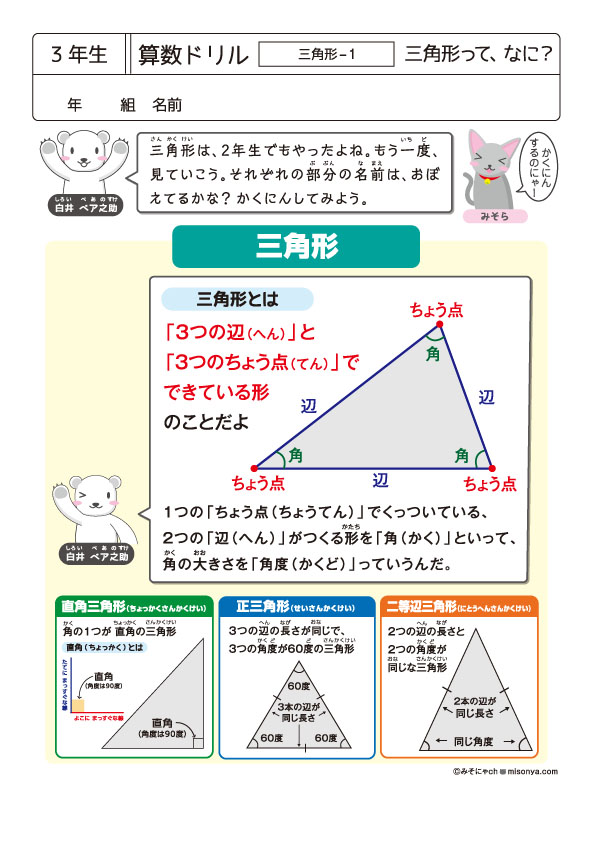



無料の学習プリント 小学3年生の算数ドリル 三角形 みそにゃch
角の和 1 1 つ 1 1 つの角の大きさではなく、いくつかの角の和を求めよという問題 があります。 1 1 つ 1 1 つの角の大きさは求まらないことが多く、 角を集めていくことで解決します。 角を集めるためには、三角形の外角を用います。角の大きさ 三角定規を組み合わせ てつくった角度につい て,その組み合わせた 方を読み取り,図や式 を根拠にして説明する ことができる。 三角形 形としての角の概 念を理解し,角を 切り取ったり,写 し取ったりして大 小を比べることが とができる。4年 角とその大きさ1 子どもの学習支援 by いっちに算数 動画を見せながら教えると わかりやすくなります 角を測るためには、頂点に分度器の中心をあわせることや0度の線を、図りたい形の直線に重ねる操作活動が必要です。 また目盛りの内側と外側の読みまちがいがないようにすることも
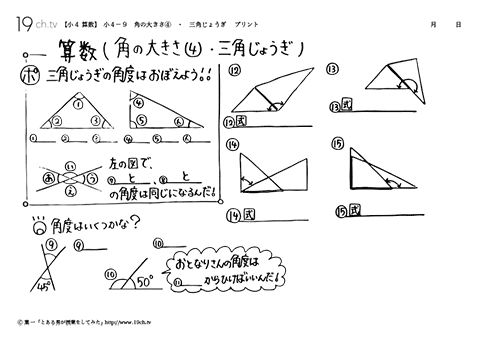



小学4年生の算数 動画 角の大きさ 三角じょうぎの問題 19ch



ラングレーの問題 整角四角形
考三角形の内角の和を,三角 定規の角の大きさを調べた り,いろいろな三角形の三 つの角を一つの点に集めた りすることを通して帰納的 に考え,説明している。 (ノート・観察) 技計算で三角形の角の大き さを求めることができる。 3 四角形の内角の和三角形の合同条件を使って、合同な三角形を見つける方法! 証明の書き方合同な三角形の証明問題の書き方を基礎から解説! 直角三角形証明問題の書き方とは?合同条件の使い方を徹底解説! 二等辺三角形の角度の求め方 厳選6問解説!表計算で三角形の角の大きさを求 めることができる。 2・ 三角形の内角の和を調べ,180°・作業的な活動 知三角形の内角の和は180°である / になることを知る。 ・説明する活動 ことを理解している。 8・ 三角形の角の大きさを求める適用 問題を解決する。
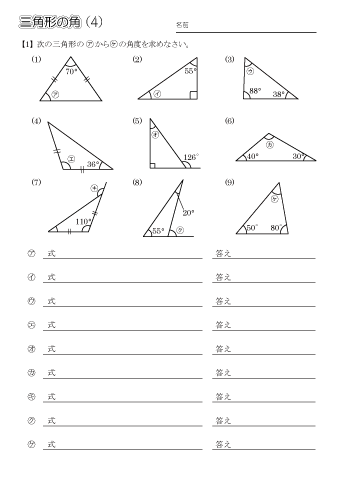



小学5年生の算数 多角形の角 三角形の角 問題プリント ちびむすドリル 小学生
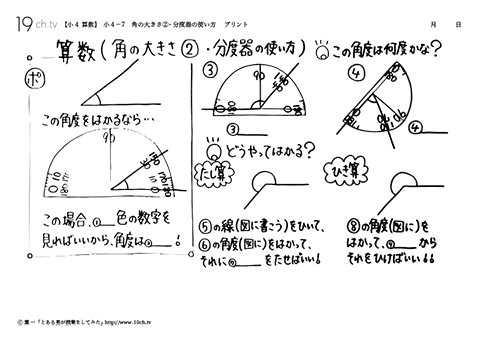



小学4年生の算数 動画 角の大きさ 分度器の使い方の問題 19ch
A=35,b=43,c=13とおくとb=43が最大辺だからBが最大角になる cosB= = = − ⇒ B=1° (4) 1,,・多角形、正多角形 ・三角形の三つの角、四角形の四つの 角の大きさの和 ・合同な図形 1年 ・形の特徴 ・形作り・分解 ・ものの位置 2年 ・三角形、四角形、正方形、長方 形、直角三角形 ・線対称や点対称 ・対応する辺の長さ ・対応する角の大きさ名前 三角形と角 (1/5) ば とうへん にあてはまる 言葉を 書きましょう。 へん ①2つの辺の長さが 等しい 三角形を と いいます。 ひと へん ひと ②3つの辺の長さが 等しい 三角形を と いいます。 へん ③3つの辺の長さが 2cmの 三角形は です。 へん ④2つの辺の長さが 5cmの 三角形は です。
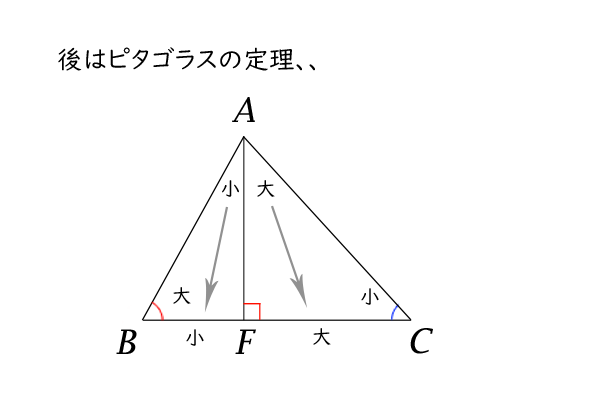



三角形の辺の長さと角の大きさの関係 高校数学マスター
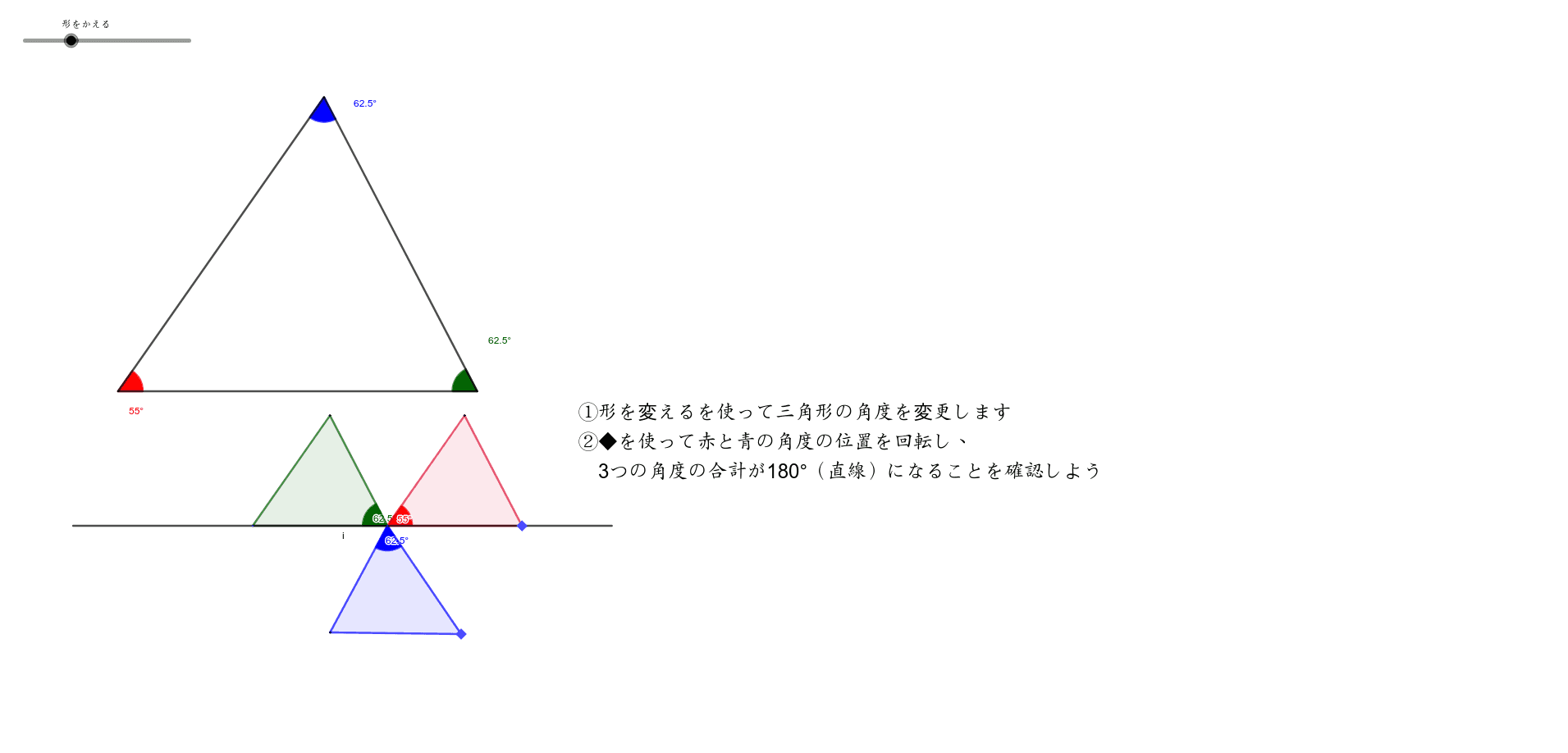



小5 三角形の角の大きさのひみつ Geogebra
A=6,b=7,c=10で計算結果が A=3618・・,B=4353・・,C=・・,h=6・・,S=66・・ if c>=a,bの場合はh=2S/cになっているが、 2*66/10=413・・になってしまう。使用法 製図用に用いられる三角定規は、角が45°・45°・90°(直角二等辺三角形)の三角定規と、角が30°・60°・90°(正三角形の半分、半正三角形)の三角定規の2枚一組となっている 。 一組の三角定規において、直角二等辺三角形の斜辺(45°45°の辺)と、半正三角形の長いほうの隣辺(90°30角 角については,第2学年で下のように不定形の紙を折る操作などを通して,直角について学習してきています。 第3学年では,この学習を発展させ,角を次のように意味づけします。 指導にあたっては,角を独立して取り扱うのではなく,三角形と関連




二等辺三角形 Wikipedia
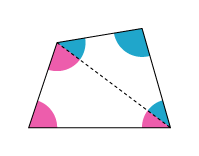



四角形の4つの角の大きさの和 5年生 算数の広場
ここでは折り紙を使って、三角定規の形をたくさん用意する方法をご紹介します。 三角定規は2枚1組になっていますね。 a 直角二等辺三角形(角が90°、45°、45°) b 直角三角形(角が90°、60°、30°) この2枚です。② 2直角は で、 1回転した 角の大きさ 4直角は です。 ① 直角とは 90度の事で と書きます。 ④ 正三角形の 一つの内角の大きさは です。 ③ 三角形の 内角の和は です。 頂点 ちょう 180° 360° 45° 45° 30° 90° 60° 90° へん三角形と四角形の角(2) ・三角形の内角の和は 180°であることを帰納的に考え,計算で三角 形の角の大きさを求める。 考 三角形の内角の和が180°であることを帰納的に考え,説明してい る。 技 未知の三角形の角の大きさを計算で求めることが



1
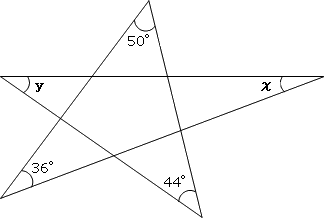



角度の求め方 算数の教え上手 学びの場 Com
調べる三角形は,前時の三角 形を3枚残しておき,それを使用するようにした。 ・ 個人で確かめた方法と結果は,「友達にもよく分かるように」を意識させて,ワークシー トに書かせるようにした。 ・ 本時では,3つの角の大きさの和が180°で あることを三角形の まもるさんたちは,上の表からわかることを発表しました。 例えば,三角形の三から2をひくと,三角形の数は1になります。 三角形の数が2倍,3倍になると, 2 いろいろな多角形の角の大きさの和を (3) 十二角形の角の大きさの和は何度ですか。角の表し方,角度の単位「度」の意味を理解する。 3.本単元の学習の系統 方形・直角三角形の概念, 三角形と四角形 ・直角の概念,長方形・正 性質,かき方 垂直・平行と四角形 ・垂直,平行の概念,かき方 ・平行線を活用してできる角の




5年算数 図形の角と合同 9 三角形の角の大きさを求めよう あなたの人生はあなたの思い描いたとおりになる
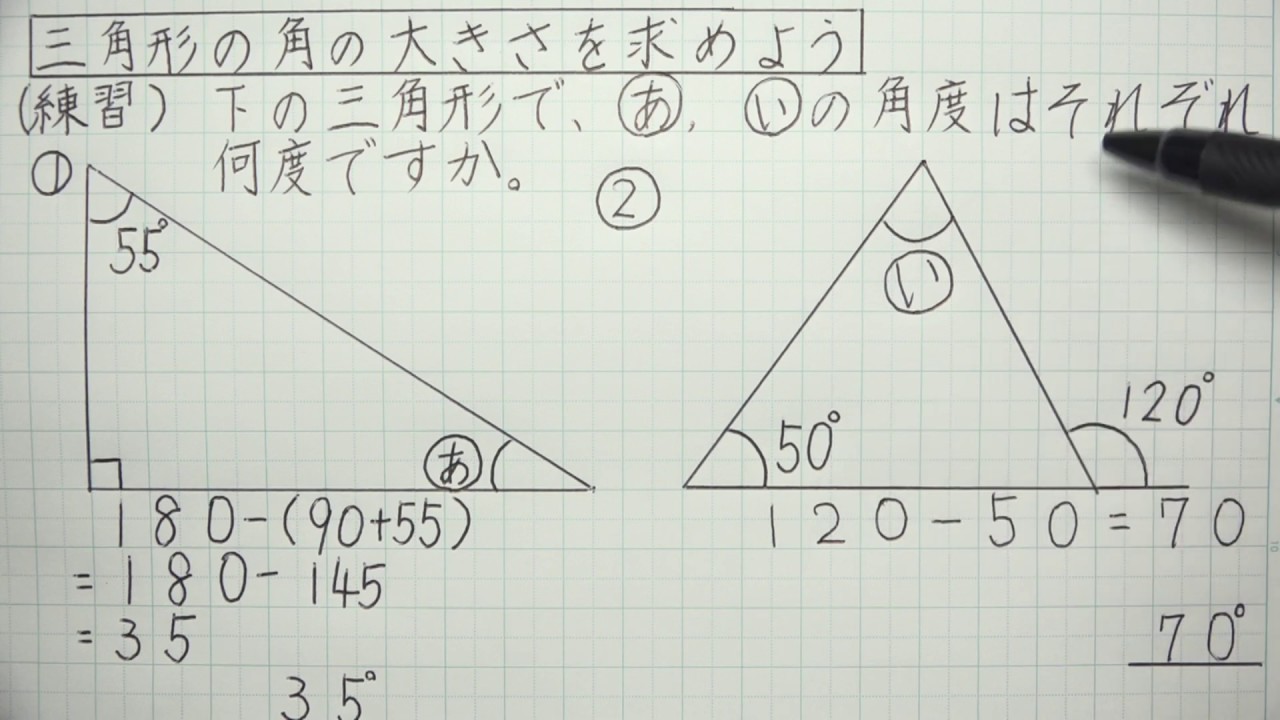



5年算数 図形の角と合同 6 三角形の角の大きさを求めよう Youtube
辺三角形や正三角形の角の大小・相等関係を確かめられる。 5.評価規準 (関心・意欲・態度) 身近にある基本的な形(三角形)を分類しようとする。 (数学的な考え方) 辺の長さによって三角形を分類して考えることができる。以上でめでたく3つの角の大きさ a 、 b 、 c が求まりました。冬の大三角は、3つの角の大きさがほとんど同じで、正三角形に近いことが分かりますね。 最後に、球面上での三角形の面積 S は、以下のようにして求められます。 (式6)同じ三角定規を2枚使ってできた 三角形の3つの角の和について 三角形で考える。 三角定規の角の大きさや分度器 →・三角定規で考えたときのように180°ではないか。 での計測結果から,意欲的に考 ・90°が3つ分ある270°よりは小さくなるはずだ。




中学数学 正三角形の角度の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
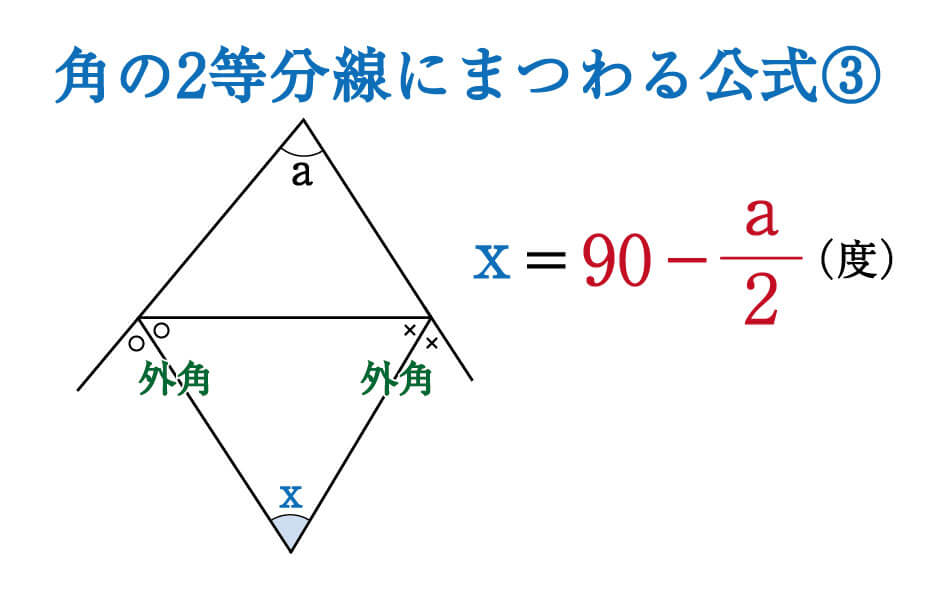



数学 角の二等分線にまつわる絶対に覚えておきたい公式 受験の秒殺テク 8 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo
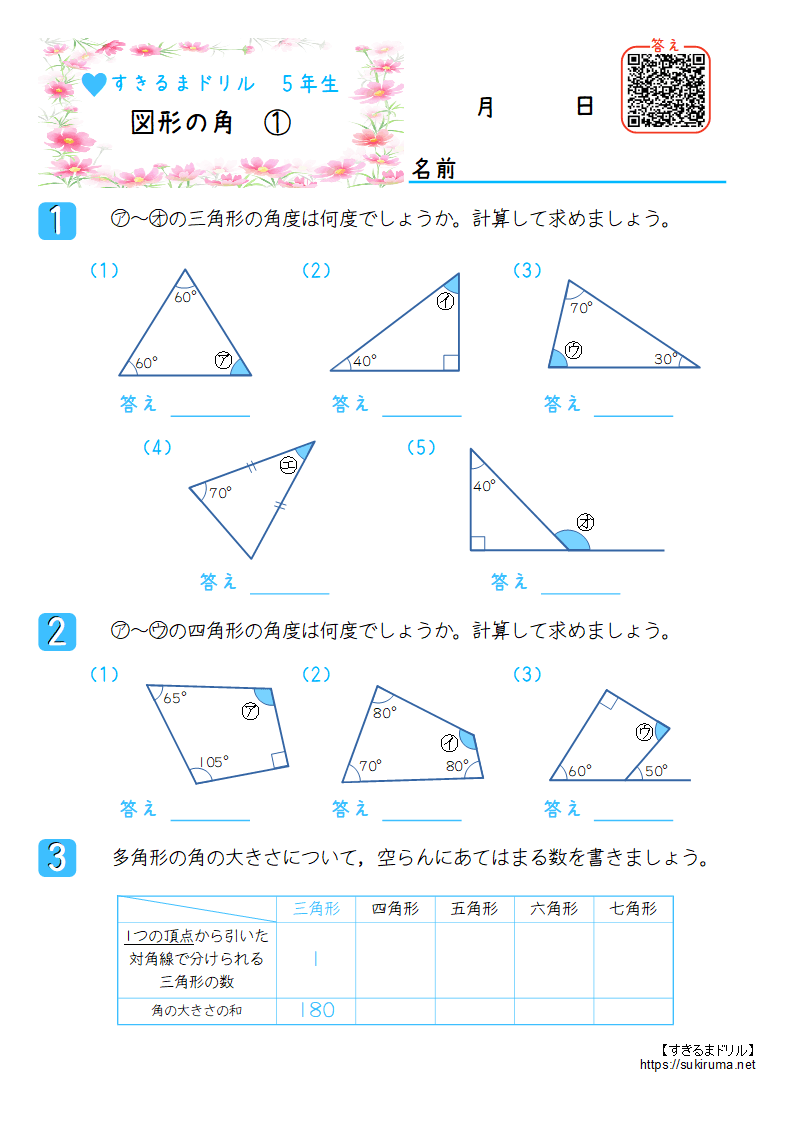



すきるまドリル 小学5年生 算数 図形の角 無料学習プリント すきるまドリル 無料学習プリント
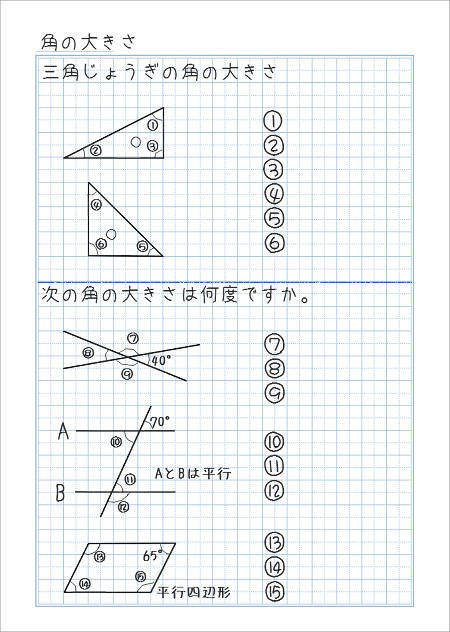



角の大きさを計算で求める自主学習ノート例 家庭学習レシピ
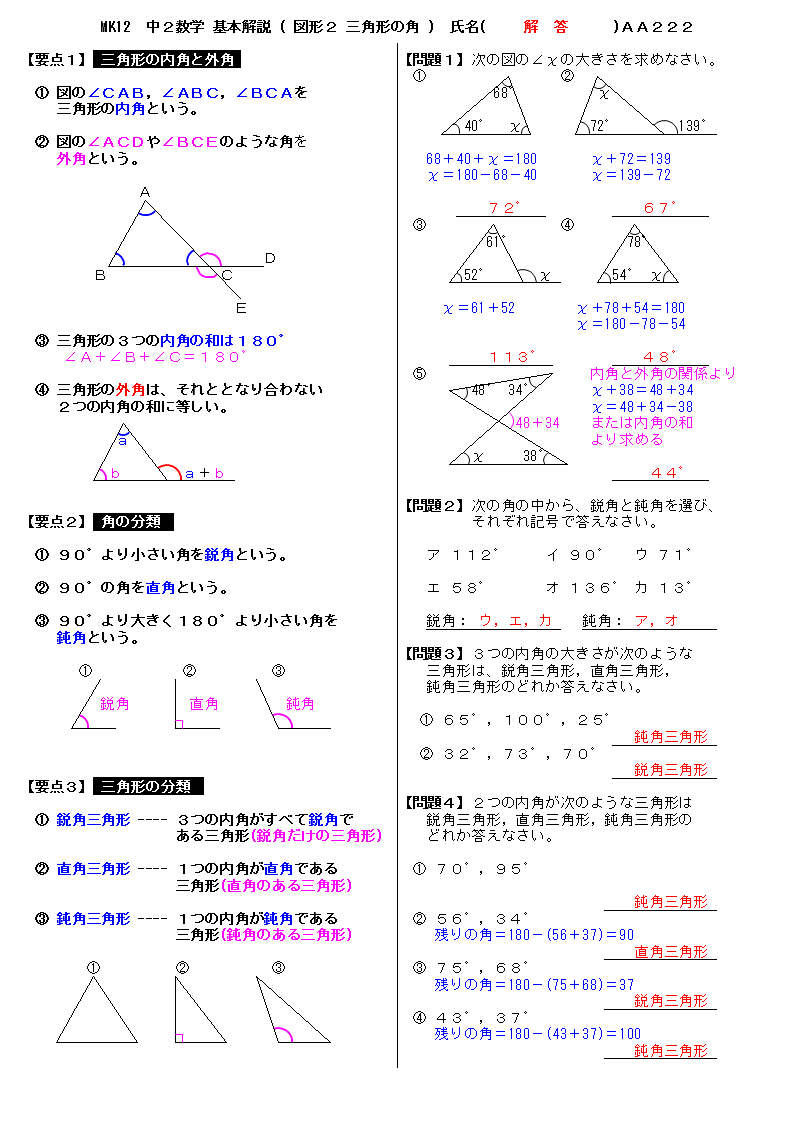



無料 中2数学 基本解説 解答プリント 222 図形2 三角形の角
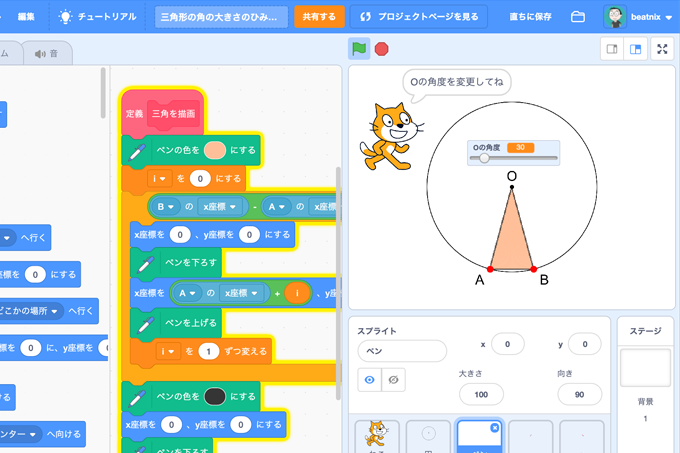



既存の教科でプログラミング授業 小学5年生 算数 三角形の角の大きさのひみつをさぐろう2 コドモとアプリ



正三角形とは 定義や面積公式 高さや角度の求め方 受験辞典



Http Www Kochinet Ed Jp Akidai1 E Kenkyu Tyukanhappyou 3 1 Pdf



Http Www City Kofu Yamanashi Jp Gakkoukyoiku Gakusui H21 Print Sp 4 3 5 Pdf
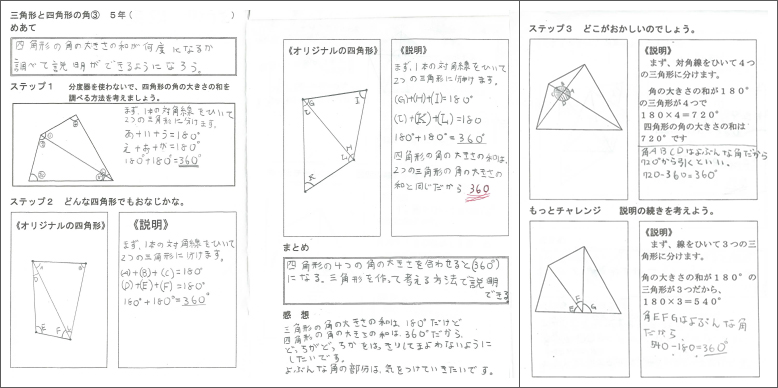



重なる形と図形の角を調べよう 図形の角と合同 第5学年 小学校 算数 My実践事例 日本文教出版




三角形の辺の長さと角の大きさの関係 数学i By ふぇるまー マナペディア
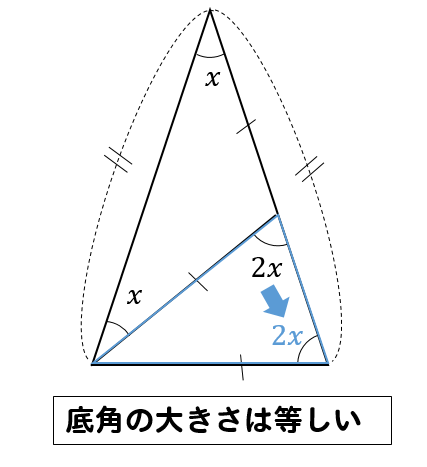



二等辺三角形の角度の求め方を問題を使って徹底解説 数スタ
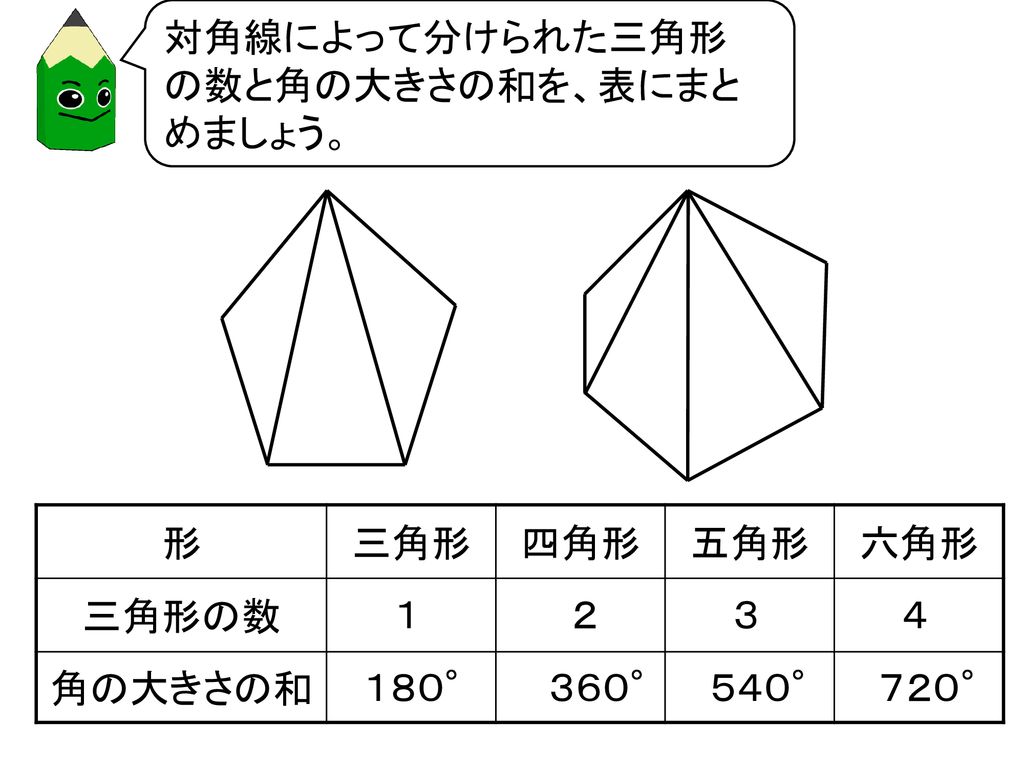



三角形や四角形ではない図形の 角の大きさの和を求めよう Ppt Download




旧バージョン 5年算数 図形の角と合同 6 三角形の3つの角の大きさの和を調べよう Youtube
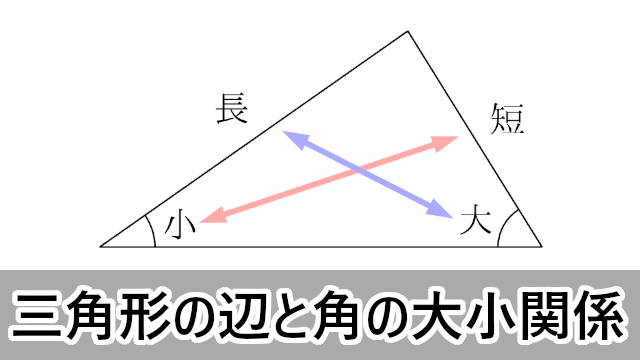



数学ia 三角形の角の大きさと辺の長さの関係 大学入試数学の考え方と解法
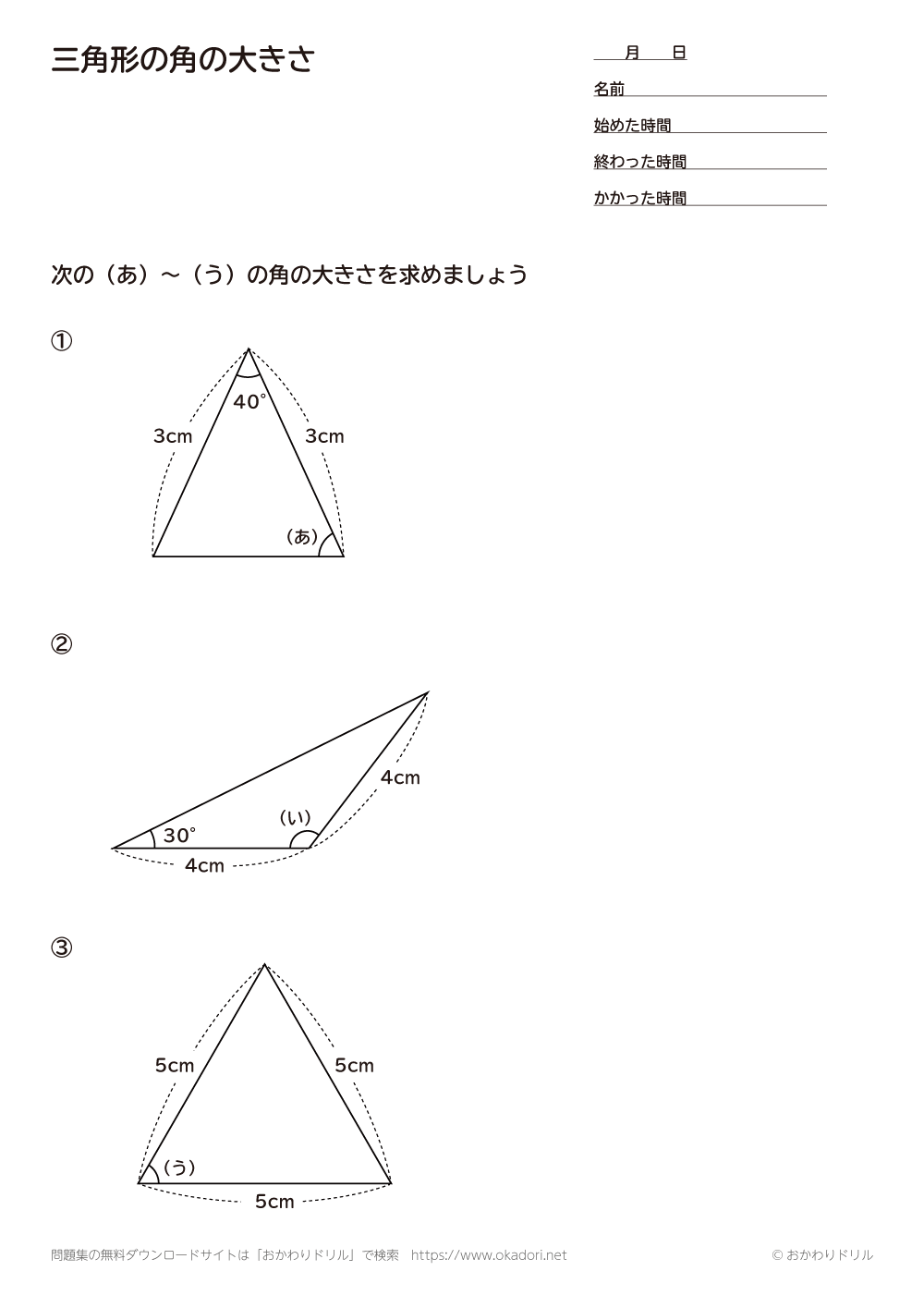



小学5年生 算数 無料問題集 三角形の角の大きさ おかわりドリル




余弦定理で角度を求める方法 数学の星




中2数学 三角形 直角三角形の合同条件の覚え方のポイントを解説 まなビタミン
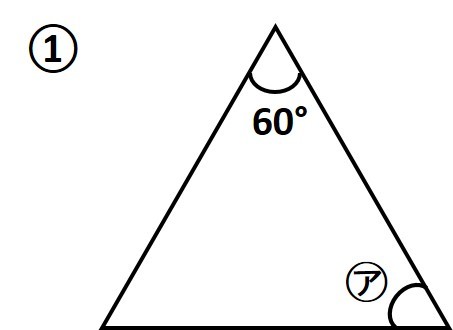



動画で学習 1 三角形 四角形の角 算数



3年算数 角の大きさ 高岡市立伏木小学校




世界一分かりやすい算数 小4 角とその大きさ
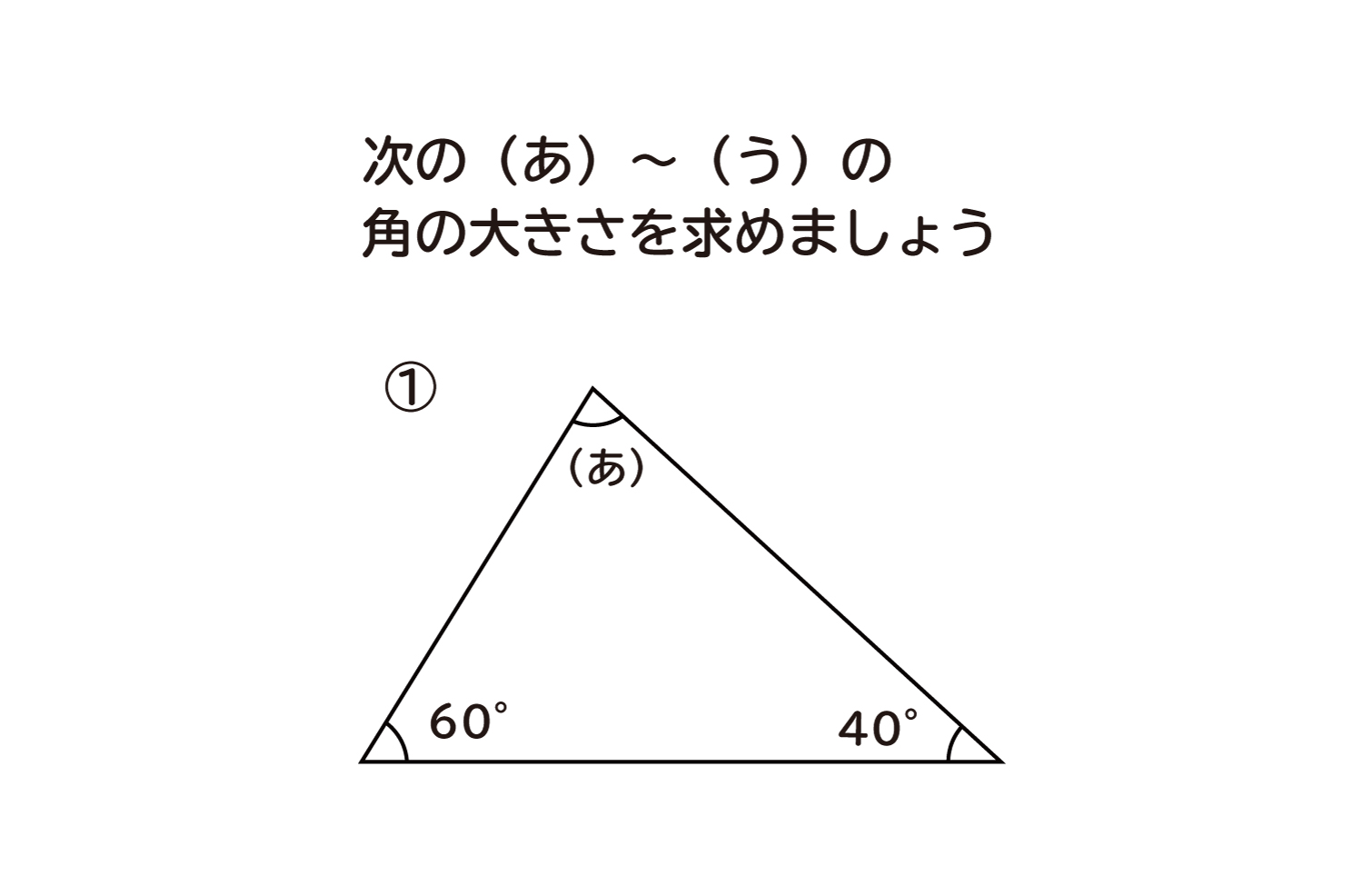



小学5年生 算数 無料問題集 三角形の角の大きさ おかわりドリル
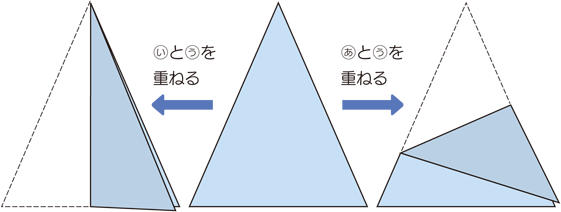



角 算数用語集



1




二等辺三角形の角を求める Youtube




図形の調べ方 三角形 役に立つ角度の求め方 苦手な数学を簡単に



1
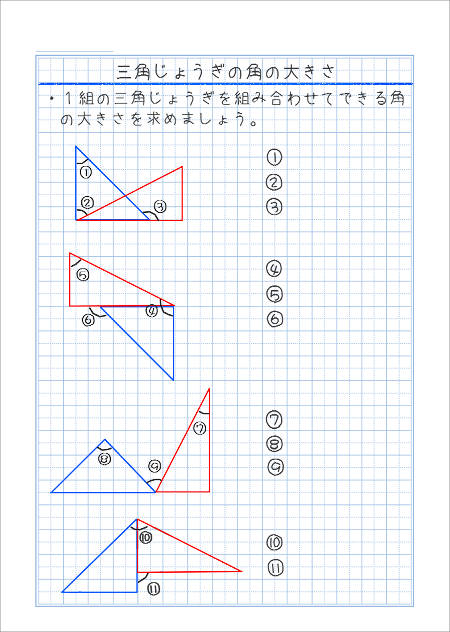



三角じょうぎの角の大きさ 家庭学習レシピ
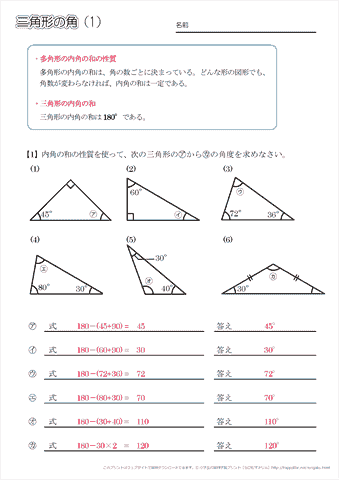



小学5年生の算数 多角形の角 三角形の角 問題プリント ちびむすドリル 小学生




高校数学 三角形の辺と角の関係 映像授業のtry It トライイット



中学数学 三角形の内角 外角 中学数学の無料オンライン学習サイトchu Su




小学5年生 正多角形 算数 Active Learning 学院



5年 三角形のふしぎ 算数イメージ動画集 大日本図書




二等辺三角形の底角は本当に等しいのか ひと筋縄ではいかない証明 ブルーバックス編集部 ブルーバックス 講談社 1 4




2番が分かりません 教えて下さい Clear




の角度を求める 求角問題です 答えは75度らしいのですがよくわかりません Clear




数学 角の二等分線にまつわる絶対に覚えておきたい公式 受験の秒殺テク 8 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




5年生算数 図形の角 四角形の角の大きさの和 指導実践 ネコ好きな学校の先生の日常



動画で学習 1 三角形 四角形の角 算数




中高生必読 知らないとヤバい二等辺三角形の知識 定義 角度 面積 高校生向け受験応援メディア 受験のミカタ




二等辺三角形の定義 角度の性質を使った証明問題などを解説 遊ぶ数学




小学5年生の算数 多角形の角 三角形の角 問題プリント ちびむすドリル 小学生




三角形の内角の和が180 なのはなぜ 小学生に教えるための解説 数学fun



1
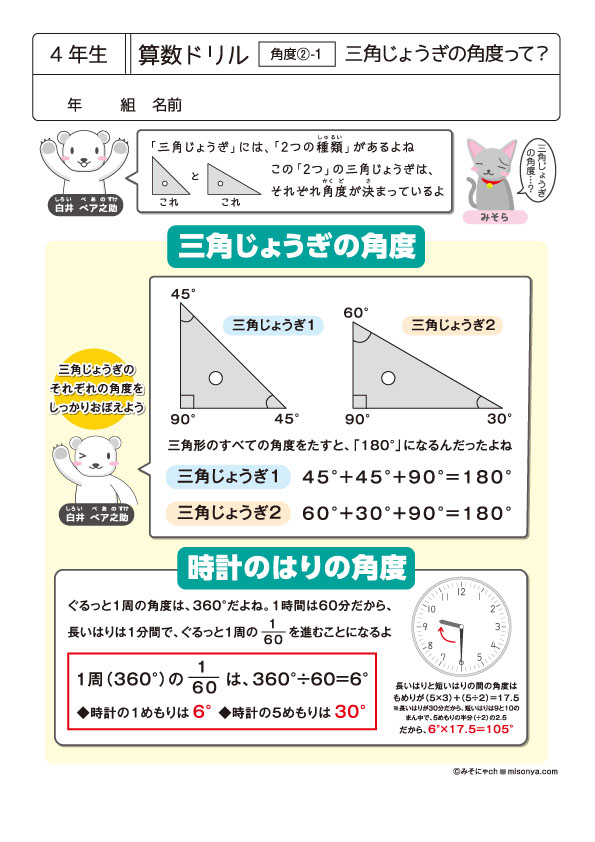



無料の学習プリント 小学4年生の算数ドリル 角度2 三角定規と時計の針 みそにゃch




中2数学です 角xの大きさの求め方を教えてください 同じ印のついて 数学 教えて Goo




世界一分かりやすい算数 小3 三角形
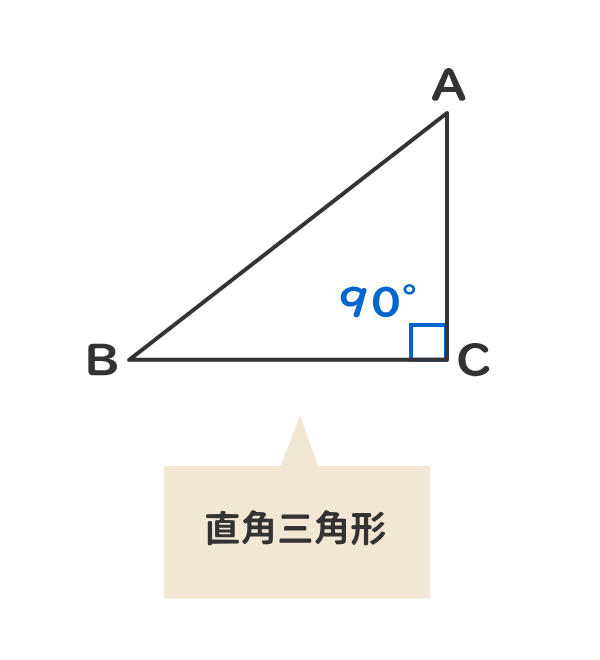



二つの特別な直角三角形の角度と辺の長さの比の関係を暗記しよう 電験3種web
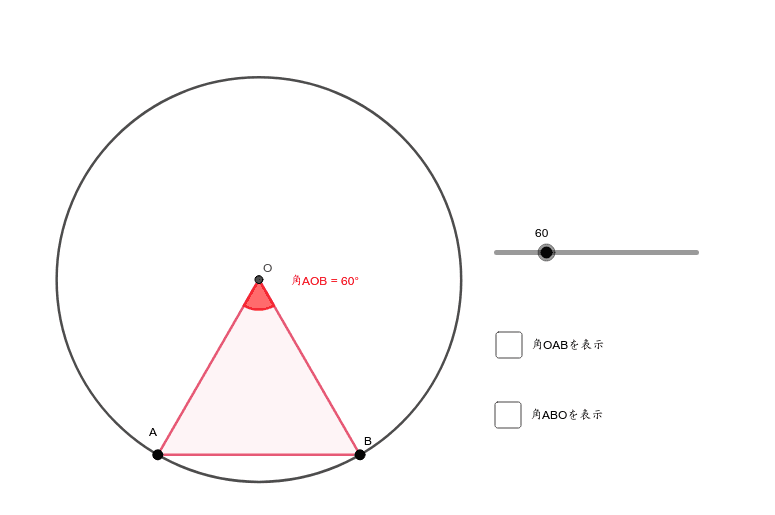



小5 二等辺三角形の角の大きさのひみつ Geogebra




三角形の角度を求める問題 小学生 中学生の勉強



Math 平行と合同 角の二等分線と角度 働きアリ
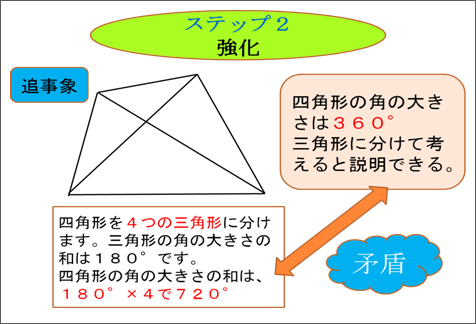



重なる形と図形の角を調べよう 図形の角と合同 第5学年 小学校 算数 My実践事例 日本文教出版




三角形のそれぞれの角の大きさ スクールプレゼンター教材共有サイト スクプレ道場
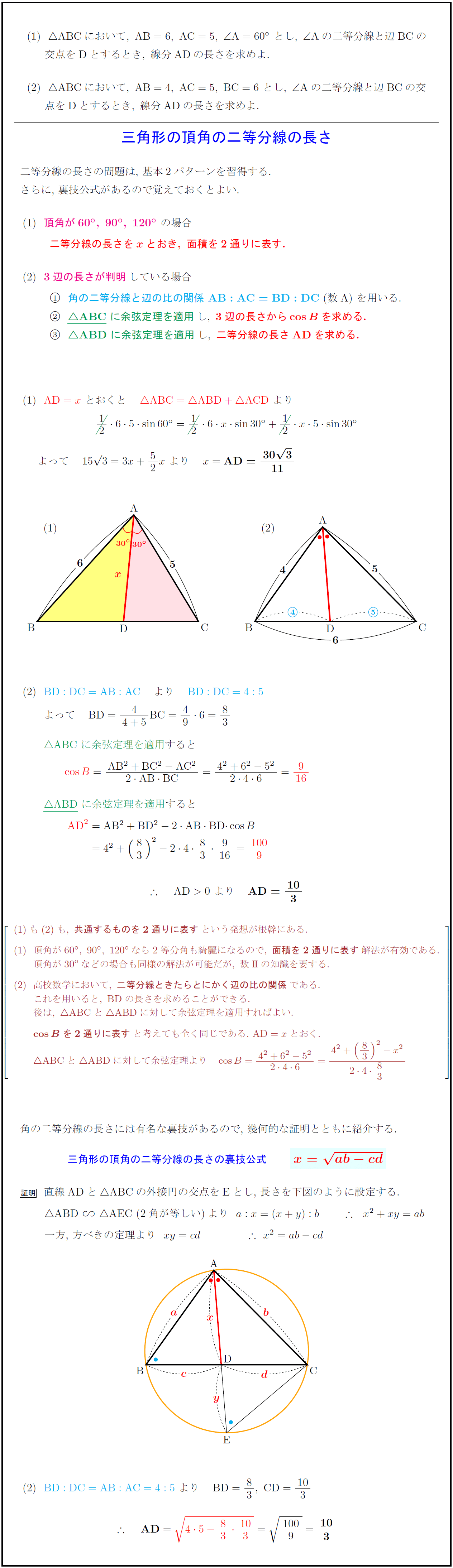



高校数学 三角形の頂角の二等分線の長さ 基本2パターン 裏技公式 X Ab Cd とその証明 受験の月




多角形 四角形 五角形 六角形 の内角の和の公式 問題の解き方 数学fun



二等辺三角形とは 定義や定理 角度 辺の長さ 面積の求め方 受験辞典



合同な図形2
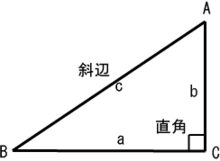



直角三角形 Wikipedia




最大角を求める問題 怜悧玲瓏 高校数学を天空から俯瞰する




旧バージョン 5年算数 図形の角と合同 6 三角形の角の大きさを求めよう Youtube




私なりに考えた三角定規を使った角の大きさの比べ方 発達ゆっくりっ子の365日



Www Pref Kanagawa Jp Documents S5 S09 02 K A Pdf




角のせいしつ 平行線と角 分度器 三角定規 小学生4年生 小学生の算数が基礎から子どもは学べ 大人は教えられる算数サイト



4年算数 角とその大きさ 1 分度器の使い方




角度の求め方 算数の教え上手 学びの場 Com
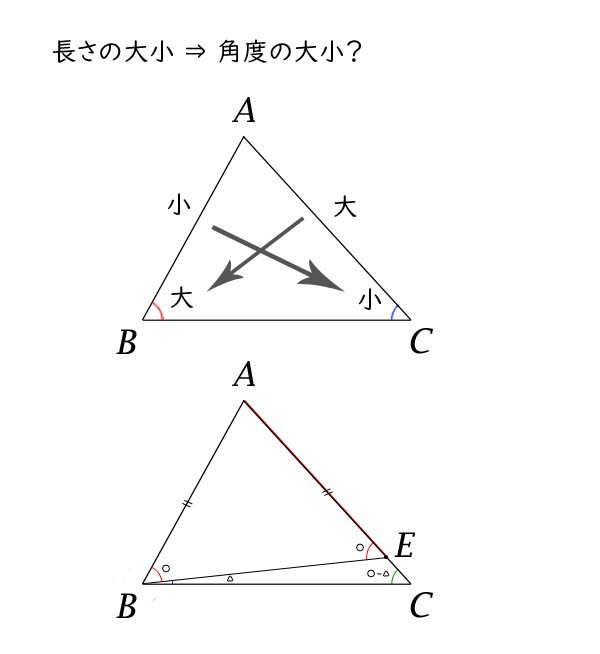



三角形の辺の長さと角の大きさの関係 高校数学マスター




三角形の角度を求める問題 小学生 中学生の勉強
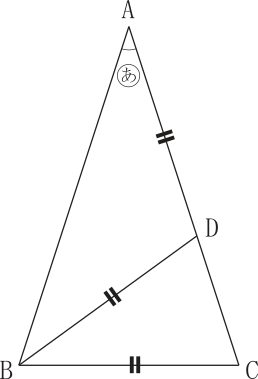



二等辺三角形 In 二等辺三角形 角度の問題 算数の広場
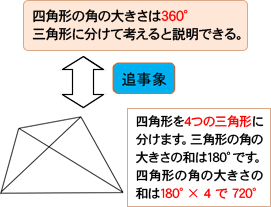



重なる形と図形の角を調べよう 図形の角と合同 第5学年 小学校 算数 My実践事例 日本文教出版




小5 算数 小5 31 三角形の角 Youtube




中2数学 ブーメラン型角度の求め方を解説 数スタ




算数 小4 9 角の大きさ 三角じょうぎ Youtube



3年算数三角形教え方のポイント



中学数学 正三角形の角度の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
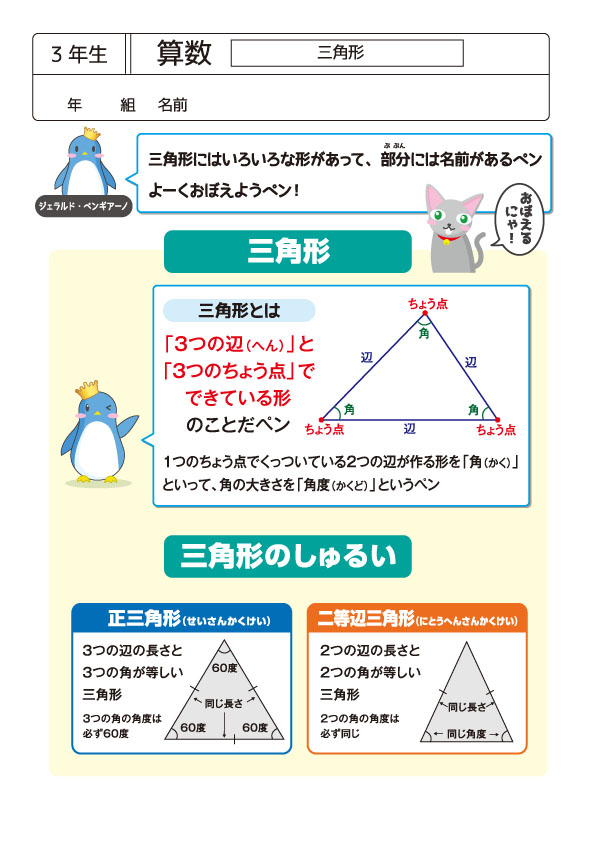



無料の学習プリント 小学3年生の算数 三角形 みそにゃch



算数 合同な図形 三角形の角 黒板log
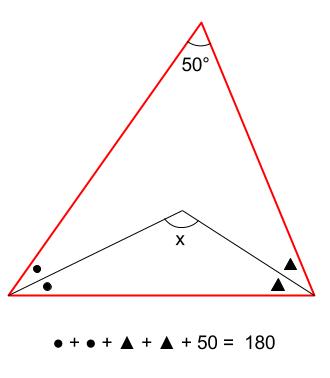



中学数学 求角と方程式 中学数学の無料オンライン学習サイトchu Su
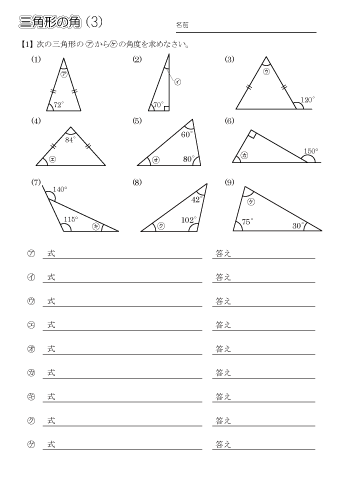



小学5年生の算数 多角形の角 三角形の角 問題プリント ちびむすドリル 小学生
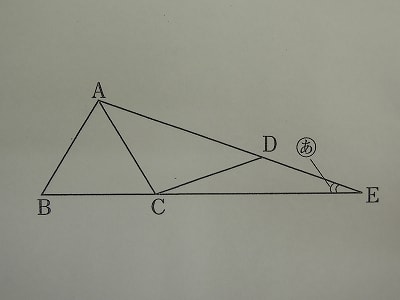



マッキーの一問必答 9 二等辺三角形の性質を利用する問題 1 マッキーのつれづれ日記




小3 算数 小3 43 三角形と角 Youtube
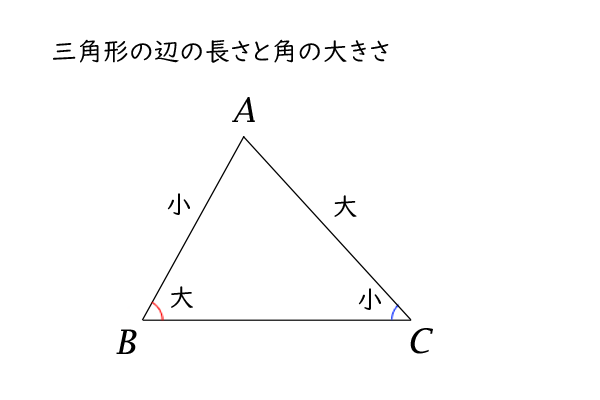



三角形の辺の長さと角の大きさの関係 高校数学マスター




小学4年生 角度の求め方は 対頂角 平行線 同位角 錯角 中学受験 そうちゃ式 受験算数 2号館 図形 速さ




8 Descubre Como Resolverlo En Qanda




内角の和 算数用語集
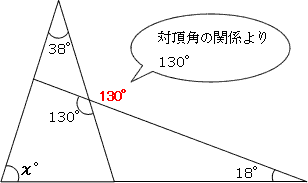



角度の求め方 算数の教え上手 学びの場 Com
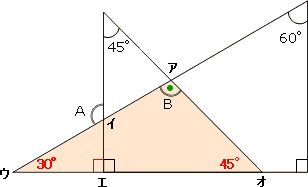



角度の求め方 算数の教え上手 学びの場 Com




正三角形や二等辺三角形の内角 Youtube
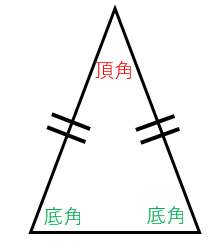



二等辺三角形の角度の求め方と例題 具体例で学ぶ数学



Www City Kofu Yamanashi Jp Gakkoukyoiku Gakusui H21 Print Sp 5 2 1 Pdf



中2数学 二等辺三角形の基礎 角の大きさ 二等分線 合同を用いた証明 授業わかるーの Byナオドット先生 中学数学のわかりやすい解説サイト



0 件のコメント:
コメントを投稿